题目内容
已知抛物线方程为
，则该抛物线的准线方程为
- A.
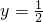
- B.
- C.y=-2
- D.y=2
D
分析：将抛物线化成标准方程得：x2=-8y，得该抛物线的顶点在原点，2p=8且抛物线开口向下，由此结合抛物线的焦点坐标和准线方程的公式，不难得到本题的答案．
解答：抛物线方程为，化成标准形式：x2=-8y
∴2p=8，得
=2，抛物线顶点在原点且开口向下，
因此，抛物线的焦点为F（-2，0），准线为y=2
故选：D
点评：本题给出抛物线方程，求它的准线方程，着重考查了抛物线的标准方程、基本概念和简单几何性质等知识，属于基础题．
分析：将抛物线化成标准方程得：x2=-8y，得该抛物线的顶点在原点，2p=8且抛物线开口向下，由此结合抛物线的焦点坐标和准线方程的公式，不难得到本题的答案．
解答：抛物线方程为
，化成标准形式：x2=-8y∴2p=8，得
=2，抛物线顶点在原点且开口向下，因此，抛物线的焦点为F（-2，0），准线为y=2
故选：D
点评：本题给出抛物线方程，求它的准线方程，着重考查了抛物线的标准方程、基本概念和简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
已知抛物线方程为y2=-4x，则它的焦点坐标为（ ）
| A、（-1，0） | B、（1，0） | C、（-2，0） | D、（2，0） |
，则该抛物线的准线方程为（ ）
