题目内容
自“钓鱼岛事件”,中日关系日趋紧张,不断升级.为了积极响“保钓行动”,学校举办了一场保钓知识大赛,共分两组.其中甲组满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的同学中,每组各任选2个同学,作为保钓行动代言人.(1)求选出的4个同学中恰有1个女生的概率;
(2)设X为选出的4个同学中女生的个数,求X的分布列和数学期望.
【答案】分析:(1)设“从甲组内选出的2个同学均为男同学;从乙组内选出的2个同学中,1个是男同学,1为女同学”为事件A,“从乙组内选出的2个同学均为男同学;甲组内选出的2个同学中1个是男同学,1个为女同学”为事件B,求得P(A),P(B),进而可得P(A+B);(2)可得X可能的取值为0,1,2,3,分别可得其概率,可得分布列,可得期望.
解答:解:(1)设“从甲组内选出的2个同学均为男同学;从乙组内选出的2个同学中,1个是男同学,1为女同学”为事件A,
“从乙组内选出的2个同学均为男同学;甲组内选出的2个同学中1个是男同学,1个为女同学”为事件B,
由于事件A?B互斥,且P(A)=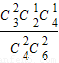 =
=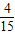 ,P(B)=
,P(B)=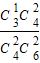 =
= ,
,
∴选出的4个同学中恰有1个女生的概率为P(A+B)=P(A)+P(B)=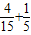 =
=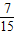 …(5分)
…(5分)
(2)由题意可知:X可能的取值为0,1,2,3,
由(1)可得:P(X=0)= ,P(X=1)=
,P(X=1)=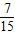 ,P(X=2)=
,P(X=2)=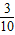 ,P(X=3)=
,P(X=3)=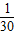
∴X的分布列为
…(10分)
∴X的数学期望:EX=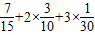 =
= …(12分)
…(12分)
点评:本题考查离散型随机变量的期望与方差,涉及排列组合公式的应用,属中档题.
解答:解:(1)设“从甲组内选出的2个同学均为男同学;从乙组内选出的2个同学中,1个是男同学,1为女同学”为事件A,
“从乙组内选出的2个同学均为男同学;甲组内选出的2个同学中1个是男同学,1个为女同学”为事件B,
由于事件A?B互斥,且P(A)=
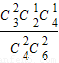 =
=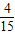 ,P(B)=
,P(B)=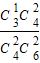 =
= ,
,∴选出的4个同学中恰有1个女生的概率为P(A+B)=P(A)+P(B)=
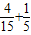 =
=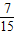 …(5分)
…(5分)(2)由题意可知:X可能的取值为0,1,2,3,
由(1)可得:P(X=0)=
 ,P(X=1)=
,P(X=1)=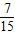 ,P(X=2)=
,P(X=2)=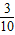 ,P(X=3)=
,P(X=3)=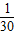
∴X的分布列为
| X | 1 | 2 | 3 | |
| P |  | 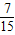 | 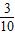 | 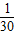 |
∴X的数学期望:EX=
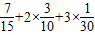 =
= …(12分)
…(12分)点评:本题考查离散型随机变量的期望与方差,涉及排列组合公式的应用,属中档题.

练习册系列答案
相关题目