题目内容
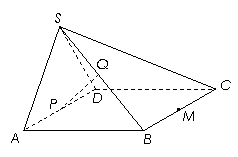
如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,且
为正方形,且![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
,![]() 为
为![]() 中点,在棱
中点,在棱![]() 上是否存在点
上是否存在点![]() , 使得平面
, 使得平面![]() ⊥平面
⊥平面![]() ,并证明你的结论.
,并证明你的结论.
 |
证明:(Ⅰ)因为四边形![]() 为正方形,则
为正方形,则![]() . …………………1分
. …………………1分
又平面![]() 平面
平面![]() ,
,
且面![]() 面
面![]() ,
,
所以![]() 平面
平面![]() . ………………………………………………………3分
. ………………………………………………………3分
 |
(Ⅱ)取SC的中点R,连QR, DR.
由题意知:PD∥BC且PD=![]() BC.…………………4分
BC.…………………4分
在![]() 中,
中,![]() 为
为![]() 的中点,R为SC的中点,
的中点,R为SC的中点,
所以QR∥BC且QR=![]() BC.
BC.
所以QR∥PD且QR=PD,
则四边形![]() 为平行四边形. …………………………………………………7分
为平行四边形. …………………………………………………7分
所以PQ∥DR.又PQ![]() 平面SCD,DR
平面SCD,DR![]() 平面SCD,
平面SCD,
所以PQ∥平面SCD. ……………………………………………………………10分
(Ⅲ)存在点![]() 为
为![]() 中点,使得平面
中点,使得平面![]()
![]() 平面
平面![]() . ………………11分
. ………………11分
连接![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,
,
因为![]() ,并且
,并且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又因为![]() 为
为![]() 中点,
中点,
所以![]() .………………………………………………………………………12分
.………………………………………………………………………12分
因为平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =
=![]() ,并且
,并且![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() , ……………………………………………………13分
, ……………………………………………………13分
又因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .……………………………………………………14分
.……………………………………………………14分

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.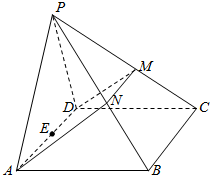 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥
如图,在四棱锥 试确定
试确定