Question

知在平面直角坐标系中，O(0，0)，M(1，

1

2

)，N(0，1)，Q(1，

2

)．若动点P（x，y）满足不等式，0≤

OP

•

OM

≤1，0≤

OP

•

ON

≤1则|

OP

•

OQ

|的最大值为

1

2

+

2

．

Answer 1

分析：利用向量的坐标求法求出各个向量的坐标，利用向量的数量积公式求出各个数量积代入已知不等式得到P的坐标满足的不等式，将|

OP

•

OQ

|的值用不等式组中的式子表示，利用线性规划求出它的范围．

解答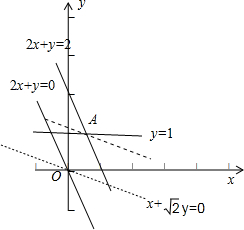：解：由题意可得

OM

=（1，

1

2

），

OP

=（x，y），

ON

=（0，1），

OQ

=（1，

2

）．
∵0≤

OP

•

OM

≤1，0≤

OP

•

ON

≤1，则  0≤x+

1

2

y≤1 且 0≤y≤1，即 0≤2x+y≤2且 0≤y≤1．
∴

OP

•

OQ

=x+

2

y，本题即求目标函数z=|x+

2

y|的最大值，故只要求得w=x+

2

y 的最值即可得到z 的最大值．
画出可行域，如图所示：
故当直线w=x+

2

y过原点O（0，0）时，w最小为0． 当直线w=x+

2

y过原点A（

1

2

，1）时，w最大为

1

2

+

2

．
故目标函数z=|x+

2

y|的最大值为

1

2

+

2

，
故答案为 

1

2

+

2

．

点评：本题考查向量的坐标形式的数量积公式、简单的线性规划问题，属于中档题．