题目内容
已知函数g(x)=ax2-2ax+b+1(a>0)在区间[2,3]上有最大值4和最小值1.设f(x)=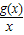 .
.(1)求a、b的值;
(2)若不等式f(2x)-k•2x≥0在x∈[-1,1]上有解,求实数k的取值范围.
【答案】分析:(1)由函数g(x)=a(x-1)2+1+b-a,a>0,所以g(x)在区间[2,3]上是增函数,故 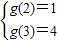 ,
,
由此解得a、b的值.
(2)不等式可化为 2x+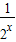 -2≥k•2x,故有 k≤t2-2t+1,t∈[
-2≥k•2x,故有 k≤t2-2t+1,t∈[ ,2],求出h(t)=t2-2t+1的最大值,
,2],求出h(t)=t2-2t+1的最大值,
从而求得k的取值范围.
解答:解:(1)函数g(x)=ax2-2ax+b+1=a(x-1)2+1+b-a,
因为a>0,所以g(x)在区间[2,3]上是增函数,故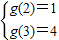 ,解得
,解得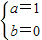 . ….(6分)
. ….(6分)
(2)由已知可得f(x)=x+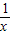 -2,所以,不等式f(2x)-k•2x≥0可化为 2x+
-2,所以,不等式f(2x)-k•2x≥0可化为 2x+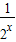 -2≥k•2x,
-2≥k•2x,
可化为 1+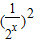 -2•
-2•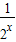 ≥k,令t=
≥k,令t=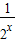 ,则 k≤t2-2t+1.
,则 k≤t2-2t+1.
因 x∈[-1,1],故 t∈[ ,2].故k≤t2-2t+1在t∈[
,2].故k≤t2-2t+1在t∈[ ,2]上能成立.
,2]上能成立.
记h(t)=t2-2t+1,因为 t∈[ ,2],故 h(t)max =h(2)=1,
,2],故 h(t)max =h(2)=1,
所以k的取值范围是(-∞,1]. …(14分)
点评:本题主要考查求二次函数在闭区间上的最值,函数的零点与方程根的关系,函数的恒成立问题,属于中档题.
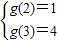 ,
,由此解得a、b的值.
(2)不等式可化为 2x+
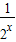 -2≥k•2x,故有 k≤t2-2t+1,t∈[
-2≥k•2x,故有 k≤t2-2t+1,t∈[ ,2],求出h(t)=t2-2t+1的最大值,
,2],求出h(t)=t2-2t+1的最大值,从而求得k的取值范围.
解答:解:(1)函数g(x)=ax2-2ax+b+1=a(x-1)2+1+b-a,
因为a>0,所以g(x)在区间[2,3]上是增函数,故
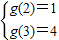 ,解得
,解得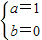 . ….(6分)
. ….(6分)(2)由已知可得f(x)=x+
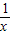 -2,所以,不等式f(2x)-k•2x≥0可化为 2x+
-2,所以,不等式f(2x)-k•2x≥0可化为 2x+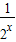 -2≥k•2x,
-2≥k•2x,可化为 1+
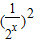 -2•
-2•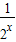 ≥k,令t=
≥k,令t=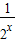 ,则 k≤t2-2t+1.
,则 k≤t2-2t+1.因 x∈[-1,1],故 t∈[
 ,2].故k≤t2-2t+1在t∈[
,2].故k≤t2-2t+1在t∈[ ,2]上能成立.
,2]上能成立.记h(t)=t2-2t+1,因为 t∈[
 ,2],故 h(t)max =h(2)=1,
,2],故 h(t)max =h(2)=1,所以k的取值范围是(-∞,1]. …(14分)
点评:本题主要考查求二次函数在闭区间上的最值,函数的零点与方程根的关系,函数的恒成立问题,属于中档题.

练习册系列答案
相关题目