Question

等差数列{a_n}的前n项和为S_n,且S₅=45，S₆=60．

(Ⅰ)求{a_n}的通项公式a_n；

(Ⅱ)若数列{a_n}满足b_n+1-b_n=a_n(n∈N^*)，且b₁=3，求数列{}的前n项和T_n．

Answer 1

解：(1)设等差数列{a_n}的公差为d，依题意，

由S₅=45，S₆=60，

得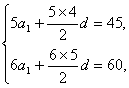解得a₁=5,d=2．

∴a_n=5+2(n-1)=2n+3．

(Ⅱ)由b_n+1-b_n=a_n，得b_n-b_n-1=2(n-1)+3=2n+1．

∴b_n= b₁+(b₂-b₁)+(b₃-b₂)+…+(b_n-b_n-1)

=3+5+7+…+(2n+1)

==n(n+2)．

∴,

T_n=

=.