题目内容
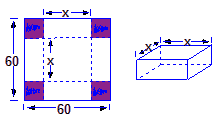
在边长为
解:设箱底边长为x,则箱高h=![]() .?
.?
∴箱子容积V(x)=x2·h=x2·![]() =
=![]() (0<x<60).?
(0<x<60).?
令V′(x)=![]() (120x-3x2)=
(120x-3x2)=![]() x(40-x)=0.?
x(40-x)=0.?
解得x1=0(舍去),x2=40.
V(40)=16 000.?
当x过小(接近0)或过大(接近60)时,V→0即箱子容积很小.?
∴16 000是最大值.?
答:当箱底边长为
温馨提示
日常生活中,常会用到什么条件下可使材料最省,时间最少,效率最高等问题.往往可以归结为求函数的最值问题.

练习册系列答案
相关题目