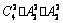题目内容
将4个不同小球放入甲、乙两个盒中,每盒至少放一个小球.下列不同放法列式正确的是
- A.C41•C31×22
- B.2C41+C42
- C.24-1
- D.C42•A22•A22
B
分析:若一个盒子中有一个球,另一个盒子中有3个球,共有的方法数为 2C41C33种,若每一个盒子中有2个球,则共有的方法数为C42种.根据分类计数原理,相加即得所求.
解答:先把4个小球分到甲、乙两个盒中,若一个盒子中有一个球,另一个盒子中有3个球,共有的方法数为 2C41C33种.
若每一个盒子中有2个球,则共有的方法数为C42种.
根据分类计数原理,所有的方法数为2C14C33+C42.
故选B.
点评:本题主要考查排列、组合以及简单计数原理的应用,体现了分类讨论的数学思想.
分析:若一个盒子中有一个球,另一个盒子中有3个球,共有的方法数为 2C41C33种,若每一个盒子中有2个球,则共有的方法数为C42种.根据分类计数原理,相加即得所求.
解答:先把4个小球分到甲、乙两个盒中,若一个盒子中有一个球,另一个盒子中有3个球,共有的方法数为 2C41C33种.
若每一个盒子中有2个球,则共有的方法数为C42种.
根据分类计数原理,所有的方法数为2C14C33+C42.
故选B.
点评:本题主要考查排列、组合以及简单计数原理的应用,体现了分类讨论的数学思想.

练习册系列答案
相关题目
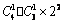 B.
B.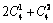
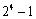 D.
D.