题目内容
已知向量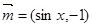 ,向量
,向量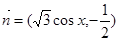 ,函数
,函数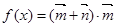 .
.
(1)求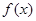 的最小正周期
的最小正周期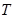 ;
;
(2)已知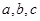 分别为
分别为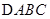 内角
内角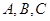 的对边,
的对边,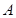 为锐角,
为锐角,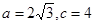 ,且
,且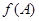 恰是
恰是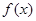 在
在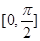 上的最大值,求
上的最大值,求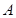 和
和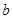 .
.
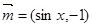 ,向量
,向量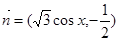 ,函数
,函数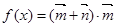 .
.(1)求
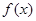 的最小正周期
的最小正周期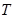 ;
;(2)已知
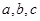 分别为
分别为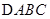 内角
内角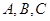 的对边,
的对边,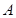 为锐角,
为锐角,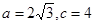 ,且
,且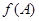 恰是
恰是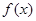 在
在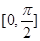 上的最大值,求
上的最大值,求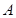 和
和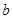 .
.(1) ;(2)
;(2)

 ;(2)
;(2)

试题分析:(1)首先根据向量和的坐标运算和向量数量积的坐标表示将函数
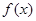 的解析式化为
的解析式化为
 的形式,再利用
的形式,再利用 和
和 的关系求周期;(2)先根据
的关系求周期;(2)先根据 确定
确定 的取值范围,再结合
的取值范围,再结合 的图像求出
的图像求出 的范围,进而求
的范围,进而求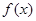 在
在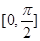 上的最大值即
上的最大值即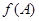 ,进而确定
,进而确定 ,此时三角形知道两边和其中一边的对角,利用余弦定理列关于
,此时三角形知道两边和其中一边的对角,利用余弦定理列关于 的方程,解之即可.
的方程,解之即可.试题解析:(1)
 ,
,

 ,
,
(2)由(1)知:
 ,
, 时,
时,
 当
当 时
时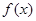 取得最大值
取得最大值 ,此时
,此时 .
.  由
由 得
得
由余弦定理,得
 ∴
∴ , ∴
, ∴ .
. 型函数的值域;3、余弦定理.
型函数的值域;3、余弦定理.
练习册系列答案
相关题目
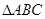 中,
中,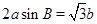 ,
, 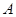 的大小;
的大小;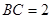 时,求
时,求 )+sin2x-cos2x.
)+sin2x-cos2x.
 =0
=0 =0
=0 中,角
中,角 对应的边分别为
对应的边分别为 ,若
,若 ,
, ,
, ,则
,则 =( )
=( )



 中,角
中,角 所对应的边分别为
所对应的边分别为 ,
, .若
.若 ,则
,则 ( )
( )

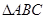 中,已知
中,已知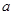 、
、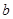 、
、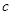 分别为
分别为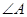 、
、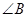 、
、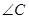 所对的边,
所对的边,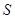 为
为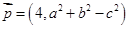 ,
,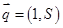 满足
满足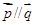 ,则
,则 .
. 中,已知点
中,已知点 在
在 边上,
边上, ,
, ,
,  ,则
,则 的长为 .
的长为 .
 中,
中, 为锐角,角
为锐角,角 所对的边分别为
所对的边分别为 ,且
,且 则
则 =___________ .
=___________ .