题目内容
已知集合A={a，b，c，d}，则A的真子集共有
15
15
个．分析：我们知道集合A={a，b，c，d}的子集共有24个，去掉其本身即得到A的真子集的个数．
解答：解：∵集合A={a，b，c，d}，
∴则A的真子集共有以下15个：∅、{a}、{b}、{c}、{d}、{a，b}、{a，c}、{a，d}、
{b，c}、{b，d}、{c，d}、{a，b，c}、{a，b，d}、{a，c，d}、{b，c，d}．
故答案是15．
∴则A的真子集共有以下15个：∅、{a}、{b}、{c}、{d}、{a，b}、{a，c}、{a，d}、
{b，c}、{b，d}、{c，d}、{a，b，c}、{a，b，d}、{a，c，d}、{b，c，d}．
故答案是15．
点评：知道含有n个不同元素的集合{a1，a2，…，an}的子集有2n个、真子集有2n-1个是解决问题的关键．
练习册系列答案
相关题目
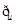B)＝R，则实数a的取值范围是 ( )