题目内容
已知函数f(x)=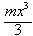 +ax2+(1-b2)x,m,a,b∈R。
+ax2+(1-b2)x,m,a,b∈R。
(l)求函数f(x)的导函数f'(x)。
(2)当m=1时,若函数f(x)是R上的增函数,求z=a+b的最小值;
(3)当a=1,b=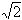 时,函数f(x)在(2,+∞)上存在单调递增区间,求m的取值范围。
时,函数f(x)在(2,+∞)上存在单调递增区间,求m的取值范围。
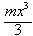 +ax2+(1-b2)x,m,a,b∈R。
+ax2+(1-b2)x,m,a,b∈R。(l)求函数f(x)的导函数f'(x)。
(2)当m=1时,若函数f(x)是R上的增函数,求z=a+b的最小值;
(3)当a=1,b=
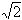 时,函数f(x)在(2,+∞)上存在单调递增区间,求m的取值范围。
时,函数f(x)在(2,+∞)上存在单调递增区间,求m的取值范围。解:(1)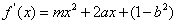 。 。 |
|
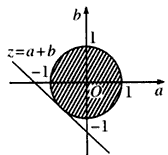
| (2)因为函数f(x)是R上的增函数, 所以f'(x)≥0在R上恒成立 则有 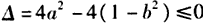 即 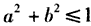 可用圆面的几何意义(如图)解得z=a+b的最小值为 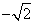 。 。 |
 |
| (3)①当m>0时,f'(x)=mx2+2x-1是开口向上的抛物线,显然f'(x)在(2,+∞)上存在子区间使得f'(x)> 0,所以m的取值范围是(0,+∞) ②当m=0时,显然成立。 ③当m<0时,f'(x)=mx2+2x-1是开口向下的抛物线,要使f'(x)在(2,+∞)上存在子区间使f'(x)>0,应满足 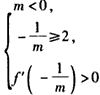 或 或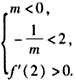 解得 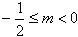 或 或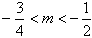 所以m的取值范围是 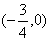 则m的取值范围是 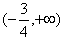 。 。 |

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|