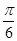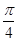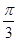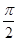题目内容
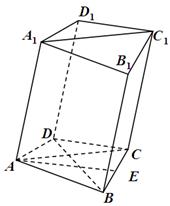
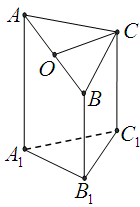
如图,在四棱柱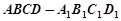 中,已知平面
中,已知平面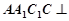 平面
平面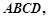 且
且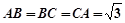 ,
,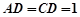 .
.
(1)求证: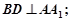
(2)若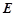 为棱
为棱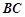 的中点,求证:
的中点,求证: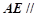 平面
平面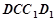 .
.
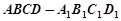 中,已知平面
中,已知平面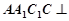 平面
平面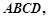 且
且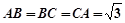 ,
,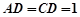 .
.
(1)求证:
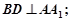
(2)若
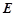 为棱
为棱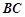 的中点,求证:
的中点,求证: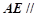 平面
平面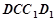 .
.⑴详见解析;⑵详见解析
试题分析:⑴要证明线线垂直
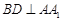 ,可转化为证明线面垂直
,可转化为证明线面垂直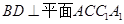 ,根据题中四边形
,根据题中四边形 中的条件
中的条件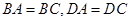 ,不难求得
,不难求得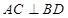 ,又由题中已知条件
,又由题中已知条件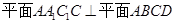 ,结合面面垂直的性质定理就可证得
,结合面面垂直的性质定理就可证得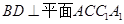 ,进而得证; ⑵要证明
,进而得证; ⑵要证明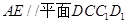 ,根据线面平行的判定定理,可转化为证明线线平行,结合题中条件可证
,根据线面平行的判定定理,可转化为证明线线平行,结合题中条件可证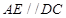 ,在四形
,在四形 中,由
中,由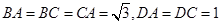 并在三角形中结合余弦定理可求出
并在三角形中结合余弦定理可求出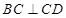 和
和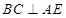 ,即可证得
,即可证得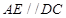 ,问题得证.
,问题得证.试题解析:⑴在四边形
 中,因为
中,因为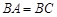 ,
, ,所以
,所以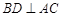 , 2分
, 2分又平面
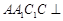 平面
平面 ,且平面
,且平面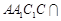 平面
平面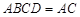 ,
,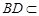 平面
平面 ,所以
,所以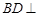 平面
平面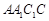 , 4分
, 4分又因为
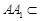 平面
平面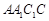 ,所以
,所以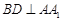 . 7分
. 7分⑵在三角形
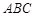 中,因为
中,因为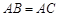 ,且
,且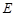 为
为 中点,所以
中点,所以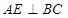 , 9分
, 9分又因为在四边形
 中,
中,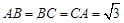 ,
,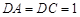 ,
,所以
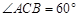 ,
, ,所以
,所以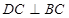 ,所以
,所以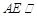
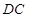 , 12分
, 12分因为
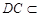 平面
平面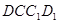 ,
,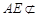 平面
平面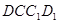 ,所以
,所以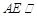 平面
平面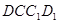 . 14分
. 14分
练习册系列答案
相关题目
 的直角边
的直角边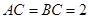 ,沿其中位线
,沿其中位线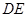 将平面
将平面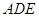 折起,使平面
折起,使平面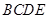 ,得到四棱锥
,得到四棱锥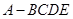 ,设
,设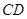 、
、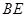 、
、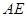 、
、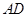 的中点分别为
的中点分别为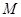 、
、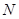 、
、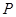 、
、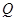 .
.


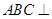 平面
平面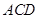 ;
;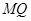 所成的角.
所成的角.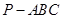 中,
中,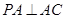 ,
,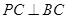 ,
,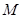 为
为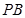 的中点,
的中点,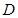 为
为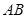 的中点,且
的中点,且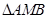 为正三角形.
为正三角形.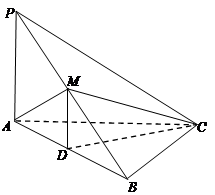
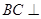 平面
平面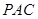 ;
;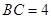 ,
,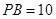 ,求点
,求点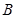 到平面
到平面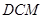 的距离.
的距离.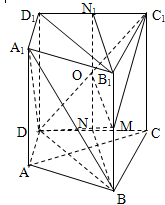
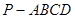 中,底面为直角梯形,
中,底面为直角梯形,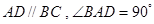 ,
,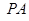 垂直于底面
垂直于底面 ,
, 分别为
分别为 的中点.
的中点.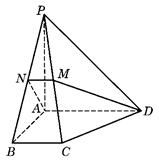
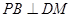 ;
;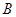 到平面
到平面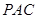 的距离.
的距离.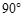 ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.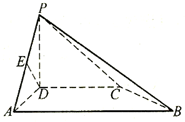
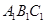 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为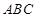 .已知
.已知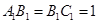 ,
,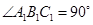 ,
,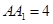 ,
,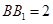 ,
,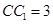 .
.
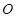 是
是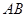 的中点,证明:
的中点,证明: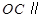 平面
平面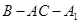 的大小;
的大小; ,那么平面
,那么平面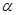 内一定存在直线平行于平面
内一定存在直线平行于平面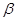 ;
; ,平面
,平面 ,
,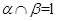 ,那么
,那么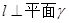 ;
;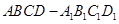 中,
中,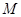 、
、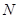 分别是
分别是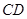 、
、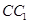 的中点,则异面直线
的中点,则异面直线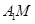 与
与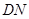 所成角的大小是( )
所成角的大小是( )