题目内容
已知函数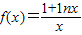 .
.(1)若函数f(x)在区间
 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围;(2)知果当x≥1时,不等式
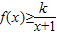 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;(3)求证:
 ,这里n∈N*,(n+1)!=1×2×3×…×(n+1),e为自然对数的底数.
,这里n∈N*,(n+1)!=1×2×3×…×(n+1),e为自然对数的底数.
【答案】分析:(1)先求出定义域,再对f(x)进行求导,利用导数研究函数f(x)的极值点问题,先求出极值点;
(2)已知条件当x≥1时,不等式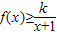 恒成立,将问题转化为k≤
恒成立,将问题转化为k≤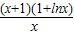 ,利用了常数分离法,只要求出
,利用了常数分离法,只要求出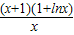 的最小值即可,可以令新的函数g(x),然后利用导数研究函数g(x)的最值问题,从而求出k的范围;
的最小值即可,可以令新的函数g(x),然后利用导数研究函数g(x)的最值问题,从而求出k的范围;
(3)利用(2)的恒成立式子,可有ln[k(k+1)]>1-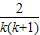 ,利用此不等式对所要证明的不等式两边进行放缩,从而进行证明;
,利用此不等式对所要证明的不等式两边进行放缩,从而进行证明;
解答:解:(1)函数f(x)的定义域为(0,+∞),f′(x)=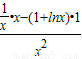 =-
=-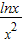 ,
,
f′(x)>0?lnx<0?0<x<1,
f′(x)<0?lnx>0?x>1,
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,函数f(x)在x=1处取得唯一的极值,
由题意,a>0,且a<1<a+ ,解得
,解得 <a<1,
<a<1,
所以实数a的取值范围为 <a<1;
<a<1;
(2)当x≥1时,f(x)≥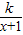 ?
?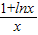 ≥
≥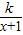 ?k≤
?k≤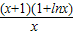 ,
,
令g(x)=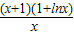 (x≥1),由题意,k≤g(x)在[1,+∞)上恒成立,
(x≥1),由题意,k≤g(x)在[1,+∞)上恒成立,
g′(x)=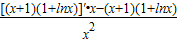 =
=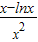 ,
,
令h(x)=x-lnx(x≥1),则h′(x)=1-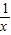 ≥0,当且仅当x=1时取等号,
≥0,当且仅当x=1时取等号,
所以h(x)=x-lnx在[1,+∞)上单调递增,h(x)≥h(1)=1>0,
因此g′(x)=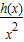 >0,g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2,
>0,g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2,
所以k≤2;
(3)由(2),当x≥1时,f(x)≥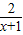 ,即
,即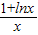 ≥
≥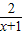 ,
,
从而lnx≥1-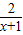 >1-
>1-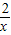 ,
,
令x=k(k+1),k∈N+,则有ln[k(k+1)]>1-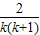 ,
,
分别令k=1,2,3,…,n(n≥2)则有ln(1×2)>1-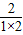 ,ln(2×3)>1-
,ln(2×3)>1-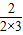 ,…,
,…,
ln[n(n-1)]>1-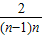 ,ln[n(n+1)]>1-
,ln[n(n+1)]>1-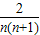 ,
,
将这个不等式左右两端分别相加,则得,
ln[1×22×32×…×n2(n+1)]>n-2[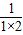 +
+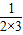 +…+
+…+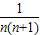 ]=n-2+
]=n-2+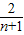 ,
,
故1×22×32×…×n2(n+1)>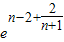 ,从而
,从而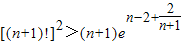 ,
,
当n=1时,不等式显然成立;
所以?n∈N+,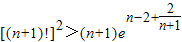 ;
;
点评:此题难度比较大,考查了利用导数研究函数的单调性和最值问题,第三问难度最大,需要对不等式的两边进行放缩,巧妙利用第(2)问的条件得到一个不等式,利用这个不等式进行放缩证明,是我们常用的方法;
(2)已知条件当x≥1时,不等式
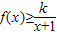 恒成立,将问题转化为k≤
恒成立,将问题转化为k≤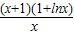 ,利用了常数分离法,只要求出
,利用了常数分离法,只要求出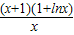 的最小值即可,可以令新的函数g(x),然后利用导数研究函数g(x)的最值问题,从而求出k的范围;
的最小值即可,可以令新的函数g(x),然后利用导数研究函数g(x)的最值问题,从而求出k的范围;(3)利用(2)的恒成立式子,可有ln[k(k+1)]>1-
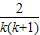 ,利用此不等式对所要证明的不等式两边进行放缩,从而进行证明;
,利用此不等式对所要证明的不等式两边进行放缩,从而进行证明;解答:解:(1)函数f(x)的定义域为(0,+∞),f′(x)=
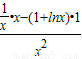 =-
=-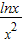 ,
,f′(x)>0?lnx<0?0<x<1,
f′(x)<0?lnx>0?x>1,
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,函数f(x)在x=1处取得唯一的极值,
由题意,a>0,且a<1<a+
 ,解得
,解得 <a<1,
<a<1,所以实数a的取值范围为
 <a<1;
<a<1;(2)当x≥1时,f(x)≥
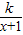 ?
?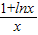 ≥
≥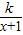 ?k≤
?k≤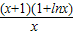 ,
,令g(x)=
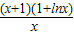 (x≥1),由题意,k≤g(x)在[1,+∞)上恒成立,
(x≥1),由题意,k≤g(x)在[1,+∞)上恒成立,g′(x)=
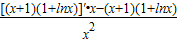 =
=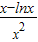 ,
,令h(x)=x-lnx(x≥1),则h′(x)=1-
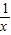 ≥0,当且仅当x=1时取等号,
≥0,当且仅当x=1时取等号,所以h(x)=x-lnx在[1,+∞)上单调递增,h(x)≥h(1)=1>0,
因此g′(x)=
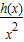 >0,g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2,
>0,g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2,所以k≤2;
(3)由(2),当x≥1时,f(x)≥
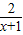 ,即
,即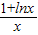 ≥
≥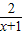 ,
,从而lnx≥1-
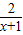 >1-
>1-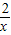 ,
,令x=k(k+1),k∈N+,则有ln[k(k+1)]>1-
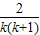 ,
,分别令k=1,2,3,…,n(n≥2)则有ln(1×2)>1-
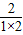 ,ln(2×3)>1-
,ln(2×3)>1-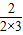 ,…,
,…,ln[n(n-1)]>1-
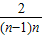 ,ln[n(n+1)]>1-
,ln[n(n+1)]>1-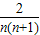 ,
,将这个不等式左右两端分别相加,则得,
ln[1×22×32×…×n2(n+1)]>n-2[
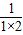 +
+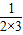 +…+
+…+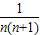 ]=n-2+
]=n-2+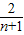 ,
,故1×22×32×…×n2(n+1)>
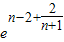 ,从而
,从而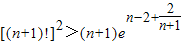 ,
,当n=1时,不等式显然成立;
所以?n∈N+,
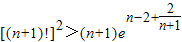 ;
;点评:此题难度比较大,考查了利用导数研究函数的单调性和最值问题,第三问难度最大,需要对不等式的两边进行放缩,巧妙利用第(2)问的条件得到一个不等式,利用这个不等式进行放缩证明,是我们常用的方法;

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目





 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。