题目内容
已知等比数列 的首项为
的首项为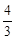 ,公比为
,公比为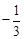 ,其前
,其前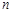 项和记为
项和记为 ,又设
,又设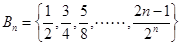
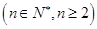 ,
, 的所有非空子集中的最小元素的和为
的所有非空子集中的最小元素的和为 ,则
,则 的最小正整数
的最小正整数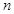 为 .
为 .
45
解析试题分析:由题意有 ,对于和
,对于和 ,我们首先把
,我们首先把 中的元素按从小到大顺序排列,当
中的元素按从小到大顺序排列,当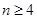 时,
时,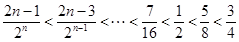 ,对于
,对于 中的任一元素
中的任一元素
 ,比它大的有
,比它大的有 个,这
个,这 个元素组成的集合的所有子集有
个元素组成的集合的所有子集有 个,把
个,把 加进这些子集形成新的集合,每个都是以
加进这些子集形成新的集合,每个都是以 为最小元素的
为最小元素的 的子集,而最小元素为
的子集,而最小元素为 的
的 的子集也只有这些,故在
的子集也只有这些,故在 中
中 出现
出现 次,所以
次,所以



 ,
, 时,
时, 适合上式,
适合上式, 时,
时, .当
.当 ,
, 不成立,当
不成立,当 时,
时, ,
, ,由于
,由于 ,
, ,
, ,所以
,所以 ,最小的
,最小的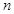 为
为 .
.
考点:子集的个数,数列的和.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列关系中,不正确的是
A. | B. | C. | D. |
若 ,则满足集合
,则满足集合 的个数为( )
的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |
若将有理数集 分成两个非空的子集
分成两个非空的子集 与
与 ,且满足
,且满足 ,
, ,
, 中的每一个元素都小于
中的每一个元素都小于 中的每一个元素,则称
中的每一个元素,则称 为有理数集的一个分割.试判断,对于有理数集的任一分割
为有理数集的一个分割.试判断,对于有理数集的任一分割 ,下列选项中,不可能成立的是( )
,下列选项中,不可能成立的是( )
A. 没有最大元素, 没有最大元素, 有一个最小元素 有一个最小元素 |
B. 没有最大元素, 没有最大元素, 也没有最小元素 也没有最小元素 |
C. 有一个最大元素, 有一个最大元素, 有一个最小元素 有一个最小元素 |
D. 有一个最大元素, 有一个最大元素, 没有最小元素 没有最小元素 |
 则
则 就称
就称 是“和谐”集合.则在集合
是“和谐”集合.则在集合 的所有非空子集中,“和谐”集合的概率是 .
的所有非空子集中,“和谐”集合的概率是 . 中最小的数是
中最小的数是 ; (2)若
; (2)若 不属于
不属于 属于
属于 则
则 ; (4)
; (4) 的解可表示为
的解可表示为 ;
; ∈A,就称A是“伙伴关系集合”,集合M=
∈A,就称A是“伙伴关系集合”,集合M= 的所有非空子集中具有伙伴关系的集合的个数是________.
的所有非空子集中具有伙伴关系的集合的个数是________. ,则集合A的真子集的个数是_____________
,则集合A的真子集的个数是_____________