题目内容
【题目】如图，在正方体ABCD – A1B1C1D1中，点E，F，G分别是棱BC，A1B1，B1C1的中点．
（1）求异面直线EF与DG所成角的余弦值；
（2）设二面角A—BD—G的大小为θ，求 |cosθ| 的值．
【答案】(1) 
(2) 
【解析】试题分析：（1）建立空间直角坐标系，进而通过计算
即可得解；
（2）计算得平面DBG和平面ABD的法向量n1和n2，通过计算cos＜n1，n2＞即可得解.
试题解析：
如图，以{
，
，
}为正交基底建立坐标系D—xyz．
设正方体的边长为2，则D(0，0，0)，A(2，0，0)，
B(2，2，0)，E(1，2，0)，F(2，1，2)，G(1，2，2)．
（1）因为
＝(2，1，2)－(1，2，0)＝(1，－1，2)，
＝ (1，2，2)，
所以·＝1×1＋(－1)×2＋2×2＝3，
||＝
＝
，||＝3．
从而cos＜，＞＝
＝
＝
，
即向量与的夹角的余弦为，
从而异面直线EF与DG所成角的余弦值为
．
（2）
＝(2，2，0)，＝ (1，2，2)．
设平面DBG的一个法向量为n1＝(x，y，z )．
由题意，得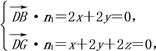 
取x＝2，可得y＝－2，z＝1．
所以n1＝(2，－2，1)．
又平面ABD的一个法向量n2＝＝(0，0，2)，
所以cos＜n1，n2＞＝
＝
＝
．
因此 |cosθ|＝．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
