题目内容
设函数 定义域为A.
定义域为A.
(1)若A=R,求实数a的取值范围;
(2)若 在x∈[1,2]上恒成立,求实数a的取值范围.
在x∈[1,2]上恒成立,求实数a的取值范围.
解:(1)因为A=R,所以ax2-2x+2>0在x∈R上恒成立.
①当a=0时,由-2x+2>0,得x<1,不成立,舍去,
②当a≠0时,由 ,得
,得 ,
,
综上所述,实数a的取值范围是 .
.
(2)依题有ax2-2x+2>4在x∈[1,2]上恒成立,
所以 在x∈[1,2]上恒成立,
在x∈[1,2]上恒成立,
令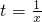 ,则由x∈[1,2],得
,则由x∈[1,2],得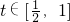 ,
,
记g(t)=t2+t,由于g(t)=t2+t在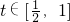 上单调递增,
上单调递增,
所以g(t)≤g(1)=2,
因此a>4
分析:(1)因为A=R,所以ax2-2x+2>0在x∈R上恒成立,根据二次函数的图象和性质,分析二次不等式恒成立时,a的取值范围,可得答案.
(2)若 在x∈[1,2]上恒成立,所以
在x∈[1,2]上恒成立,所以 在x∈[1,2]上恒成立,求出不等式右侧的最大值,即可得到实数a的取值范围.
在x∈[1,2]上恒成立,求出不等式右侧的最大值,即可得到实数a的取值范围.
点评:本题考查的知识点是对数函数的性质,恒成立问题,其中熟练掌握对数函数的单调性和定义域是解答本题的关键.
①当a=0时,由-2x+2>0,得x<1,不成立,舍去,
②当a≠0时,由
 ,得
,得 ,
,综上所述,实数a的取值范围是
 .
.(2)依题有ax2-2x+2>4在x∈[1,2]上恒成立,
所以
 在x∈[1,2]上恒成立,
在x∈[1,2]上恒成立,令
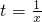 ,则由x∈[1,2],得
,则由x∈[1,2],得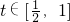 ,
,记g(t)=t2+t,由于g(t)=t2+t在
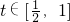 上单调递增,
上单调递增,所以g(t)≤g(1)=2,
因此a>4
分析:(1)因为A=R,所以ax2-2x+2>0在x∈R上恒成立,根据二次函数的图象和性质,分析二次不等式恒成立时,a的取值范围,可得答案.
(2)若
 在x∈[1,2]上恒成立,所以
在x∈[1,2]上恒成立,所以 在x∈[1,2]上恒成立,求出不等式右侧的最大值,即可得到实数a的取值范围.
在x∈[1,2]上恒成立,求出不等式右侧的最大值,即可得到实数a的取值范围.点评:本题考查的知识点是对数函数的性质,恒成立问题,其中熟练掌握对数函数的单调性和定义域是解答本题的关键.

练习册系列答案
相关题目
 定义域为A.
定义域为A. 在x∈[1,2]上恒成立,求实数a的取值范围.
在x∈[1,2]上恒成立,求实数a的取值范围. 定义域为A.
定义域为A. 在x∈[1,2]上恒成立,求实数a的取值范围.
在x∈[1,2]上恒成立,求实数a的取值范围. 定义域为A.
定义域为A. 在x∈[1,2]上恒成立,求实数a的取值范围.
在x∈[1,2]上恒成立,求实数a的取值范围. 定义域为A.
定义域为A. 在x∈[1,2]上恒成立,求实数a的取值范围.
在x∈[1,2]上恒成立,求实数a的取值范围.