题目内容
在底面为平行四边形的四棱锥V-ABCD中，
=2
，则三棱锥E-BCD与五面体VABED的体积之比为（ ）
| VE |
| EC |
| A、1：3 | B、1：4 |
| C、1：5 | D、1：6 |
分析：直接求出小三棱锥与E-BCD与V-DBC的体积之比，即可得到三棱锥E-BCD与五面体VABED的体积之比．
解答：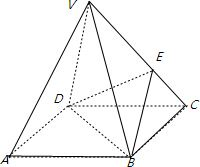
解：因为
=2
，设E到底面ABCD的距离为h则V到底面ABCD的距离为3h，
所以三棱锥与E-BCD与V-DBC的体积之比为：
，
那么三棱锥E-BCD与五面体VABED的体积之比为：
，
故选C．
解：因为| VE |
| EC |
所以三棱锥与E-BCD与V-DBC的体积之比为：
| 1 |
| 3 |
那么三棱锥E-BCD与五面体VABED的体积之比为：
| 1 |
| 5 |
故选C．
点评：本题考查棱锥的体积，考查计算能力，同底等高体积相等，同底不等高体积之比就是高之比，本题是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．
如图，在底面为平行四边形的四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，AD=1，CD=2，∠DCB=60°．
如图，在底面为平行四边形的四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，AD=1，CD=2，∠DCB=60°．