题目内容

正方体ABCD-A1B1C1D1中，点E、F分别是棱AD、CC1上的点，若AF⊥A1E则（　　）
A．AE=ADB．AE=C1FC．AE=CFD．C1F=CF

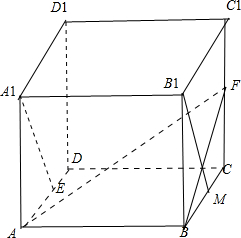
精英家教网
如图所示：在BC上取BM=AE，
则由正方体的性质可得A1E∥B1M，且A1E=B1M．
若AF⊥A1E，则 B1M⊥BF．
即直角三角形B1BM和 直角三角形BCF的三条边互相垂直，
再由B1B=BC可得直角三角形B1BM和 BCF全等，
故 CF=BM，故 CF=AE．
故选：C．
练习册系列答案
相关题目
正方体ABCD-A1B1C1D1的各顶点均在半径为1的球面上，则四面体A1-ABC的体积等于
 
．
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的：
（1）试判断A1是否在平面B1CD内；（回答是与否）
（2）求异面直线B1D1与C1D所成的角；
（3）如果用图示中这样一个装置来盛水，那么最多可以盛多少体积的水．
已知边长为6的正方体ABCD-A1B1C1D1，E，F为AD、CD上靠近D的三等分点，H为BB1上靠近B的三等分点，G是EF的中点．
（1）求A1H与平面EFH所成角的正弦值；
（2）设点P在线段GH上，
GP
GH
=λ，试确定λ的值，使得二面角P-C1B1-A1的余弦值为
10
10
．
如图所示，在棱长为2cm的正方体ABCD-A1B1C1D1中，A1B1的中点是P，过点A1作出与截面PBC1平行的截面，简单证明截面形状，并求该截面的面积．
如图，正方体ABCD-A1B1C1D1中，M是棱AB的中点，过A1，M，C三点的平面与CD所成角正弦值（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网