题目内容
正四棱锥P-ABCD的底面积为3,体积为 ,E为侧棱PC的中点,则PA与BE所成的角为
,E为侧棱PC的中点,则PA与BE所成的角为
- A.

- B.

- C.

- D.

B
分析:过顶点作垂线,交底面正方形对角线交点O,连接OE,我们根据正四棱锥P-ABCD的底面积为3,体积为 ,E为侧棱PC的中点,易求出∠OEB即为PA与BE所成的角,解三角形OEB,即可求出答案.
,E为侧棱PC的中点,易求出∠OEB即为PA与BE所成的角,解三角形OEB,即可求出答案.
解答:过顶点作垂线,交底面正方形对角线交点O,连接OE,
∵正四棱锥P-ABCD的底面积为3,体积为 ,
,
∴PO= ,AB=
,AB= ,AC=
,AC= ,PA=
,PA= ,OB=
,OB=
因为OE与PA在同一平面,是三角形PAC的中位线,
则∠OEB即为PA与BE所成的角
所以OE= ,
,
在Rt△OEB中,tan∠OEB= =
= ,
,
所以∠OEB=
故选B
点评:本题考查的知识点是异面直线及其所成的角,其中根据已知得到∠OEB即为PA与BE所成的角,将异面直线的夹角问题转化为解三角形问题是解答本题的关键.
分析:过顶点作垂线,交底面正方形对角线交点O,连接OE,我们根据正四棱锥P-ABCD的底面积为3,体积为
 ,E为侧棱PC的中点,易求出∠OEB即为PA与BE所成的角,解三角形OEB,即可求出答案.
,E为侧棱PC的中点,易求出∠OEB即为PA与BE所成的角,解三角形OEB,即可求出答案.解答:过顶点作垂线,交底面正方形对角线交点O,连接OE,
∵正四棱锥P-ABCD的底面积为3,体积为
 ,
,∴PO=
 ,AB=
,AB= ,AC=
,AC= ,PA=
,PA= ,OB=
,OB=
因为OE与PA在同一平面,是三角形PAC的中位线,
则∠OEB即为PA与BE所成的角
所以OE=
 ,
,在Rt△OEB中,tan∠OEB=
 =
= ,
,所以∠OEB=

故选B
点评:本题考查的知识点是异面直线及其所成的角,其中根据已知得到∠OEB即为PA与BE所成的角,将异面直线的夹角问题转化为解三角形问题是解答本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
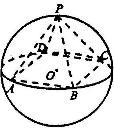 如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=
如图,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
 (2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )
(2009•温州一模)如图是正四棱锥P-ABCD的三视图,其中正视图是边长为1的正三角形,则这个四棱锥的表面积是( )