题目内容
在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC.
(Ⅰ)求角B的大小;
(Ⅱ)若点D为BC边的中点,∠CAD=![]() ,CD=1,求c的值.
,CD=1,求c的值.
考点:
余弦定理;正弦定理.
专题:
解三角形.
分析:
(Ⅰ)方法一:利用正弦定理把边化角,利用两角和差的正弦公式和诱导公式化简,由内角的范围取舍,求出角B的值,
方法二:利用余弦定理把角化边,化简后代入余弦定理的推论,求出B的余弦值,再求出B的值;
(Ⅱ)由正弦定理在△ACD,△ABD中分别列出两个方程,再由(1)和条件,用内角和定理求出∠ABC,再把条件代入方程化简,由内角的范围求出角C的值,分情况判断三角形的形状求出对应的c.
解答:
解:(Ⅰ)方法一:
∵![]() ,
,
∴![]() .
.
∵(2a﹣c)cosB=bcosC,
∴![]() .
.
∴2sinAcosB﹣sinCcosB=sinBcosC.
∴2sinAcosB=sin(B+C)=sinA.
∵A∈(0,π),∴sinA≠0.∴![]() .
.
∵B∈(0,π),∴![]() .
.
方法二:
∵(2a﹣c)cosB=bcosC,
∴![]() ,
,
化简得 a2+c2﹣b2=ca,
∴![]() ,
,
∵B∈(0,π),∴![]() ,
,
(Ⅱ)在△ACD,△ABD中,![]() .
.
由(Ⅰ)知:![]() .
.
∵点D为BC边的中点,![]() ,∴∠ABC=π﹣
,∴∠ABC=π﹣![]() =
=![]() ,
,
∴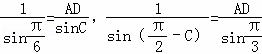 ,
,
化简得![]() ,
,
∵![]() ,∴2C∈(0,π),
,∴2C∈(0,π),
∴2C=![]() 或
或![]() ,即
,即![]() 或
或![]() ,
,
当![]() 时,△ABC为等边三角形,由CD=1可得:AB=2CD=2;
时,△ABC为等边三角形,由CD=1可得:AB=2CD=2;
当![]() 时,
时,![]() ,所以△ABD为等边三角形,由CD=1可得:AB=BD=CD=1.
,所以△ABD为等边三角形,由CD=1可得:AB=BD=CD=1.
综上得,c=2或c=1.
点评:
本题考查了正(余)弦定理在解三角形中的综合应用:边角互化或求值,以及内角和定理,倍角的正弦公式,注意求出三角函数值再求角时,一定要判断角的范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |