题目内容
在边长为5的菱形ABCD中,AC=8.现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为![]() .
.
(Ⅰ)求证:平面ABD⊥平面CBD;
(Ⅱ)若M是AB的中点,求折起后AC与平面MCD所成角的一个三角函数值.
(Ⅰ)证明:菱形![]() 中,记
中,记![]() 交点为
交点为![]() ,
, ![]() ,
,![]()
翻折后变成三棱椎![]() ,在△
,在△![]() 中,
中,
![]()
=![]()
在△![]() 中,
中,![]() ,
,
∴∠![]() =90°,即
=90°,即![]() ⊥
⊥![]() ,又
,又![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =
=![]() ,
,
∴![]() ⊥平面
⊥平面![]() , ………………………4分
, ………………………4分
又![]()
![]() 平面
平面![]() ,∴平面
,∴平面![]() ⊥平面
⊥平面![]() .
.

(Ⅱ)解:由(Ⅰ)知![]() ,
,![]() ,
,![]() 两两互相垂直,分别以
两两互相垂直,分别以![]() ,
,![]() ,
, ![]() 所在直线为坐标轴建系,则
所在直线为坐标轴建系,则![]() (0,0,4),
(0,0,4), ![]() (0,-3,0),
(0,-3,0), ![]() (4,0,0) ,
(4,0,0) ,![]() (0,3,0) ,
(0,3,0) ,![]() (0,-
(0,-![]() ,2),
,2),
![]() ,
,![]() ,………………………………8分
,………………………………8分
设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由
 , 得
, 得 ,…10分 令y=4,有
,…10分 令y=4,有![]() ……10分
……10分
设![]() 与平面
与平面![]() 所成角为θ,
所成角为θ,
![]()
∴![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() , …………………………………12分
, …………………………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

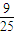 .
.