题目内容
14.过椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的左焦点F1的直线交椭圆于A,B两点,F2是右焦点,则△ABF2的周长是( )| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
分析 通过椭圆定义直接可得结论.
解答 解:由椭圆定义可知:AF1+AF2=BF1+BF2=2a=2$\sqrt{16}$=8,
∴△ABF2的周长为AF1+AF2+BF1+BF2=16,
故选:D.
点评 本题考查椭圆的定义,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
19.在样本的频率分布直方图中,共有7个小长方形,若中间一个小长方形的面积等于其它6个小长方形的面积和的$\frac{1}{4}$,且样本容量为80,则中间一组的频数为( )
| A. | 0.25 | B. | 0.5 | C. | 20 | D. | 16 |
3.下列命题错误的是( )
| A. | 命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题是“若方程x2+x-m=0没有实数根,则m≤0” | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | 命题“若xy=0,则x,y中至少有一个为0”的否命题是“若xy≠0,则x,y中至多有一个为0” | |
| D. | 对于命题p:?x∈R,使x2+x+1<0;则¬p:?x∈R,均有x2+x+1≥0 |
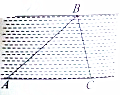 如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.
如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,现在岸边取基线AC,测得AC=120m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.