题目内容
某工厂生产某种产品,已知该产品的月生产量x(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-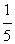 x2,且生产x吨的成本为R=50000+200x(元),问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
x2,且生产x吨的成本为R=50000+200x(元),问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
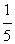 x2,且生产x吨的成本为R=50000+200x(元),问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
x2,且生产x吨的成本为R=50000+200x(元),问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本) 解:每月生产x吨时的利润为
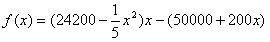
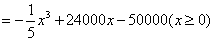 ,
,
由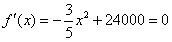 ,解得
,解得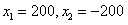 (舍去),
(舍去),
因f(x)在[0,+∞)内只有一个点x=200使f′(x)=0,
故它就是最大值点,且最大值为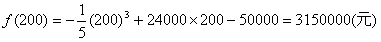 ,
,
答:每月生产200吨产品时利润达到最大,最大利润为315万元。
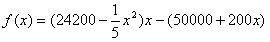
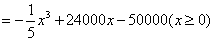 ,
,由
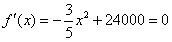 ,解得
,解得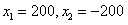 (舍去),
(舍去),因f(x)在[0,+∞)内只有一个点x=200使f′(x)=0,
故它就是最大值点,且最大值为
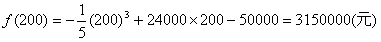 ,
, 答:每月生产200吨产品时利润达到最大,最大利润为315万元。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目