题目内容
(本小题满分12分)已知函数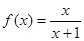 .
.
(Ⅰ)求函数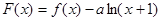 的单调递增区间;
的单调递增区间;
(Ⅱ)数列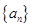 满足:
满足: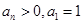 ,且
,且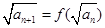 ,记数列
,记数列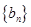 的前n项和为
的前n项和为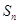 ,
,
且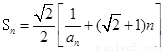 .
.
(ⅰ)求数列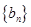 的通项公式;并判断
的通项公式;并判断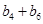 是否仍为数列
是否仍为数列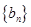 中的项?若是,请证明;否则,说明理由.
中的项?若是,请证明;否则,说明理由.
(ⅱ)设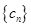 为首项是
为首项是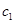 ,公差
,公差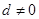 的等差数列,求证:“数列
的等差数列,求证:“数列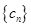 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列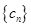 中的项”的充要条件是“存在整数
中的项”的充要条件是“存在整数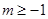 ,使
,使 ”
”
【答案】
(Ⅰ)当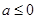 时,
时,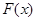 递增区间为
递增区间为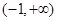 ;当
;当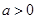 时,
时, 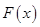 递增区间为
递增区间为
(Ⅱ)(ⅰ)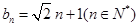 ,
,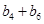 不在数列
不在数列 中
中
(ⅱ)数列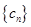 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列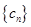 中的项的充要条件是存在整数
中的项的充要条件是存在整数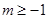 ,使
,使
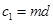
【解析】(Ⅰ)因为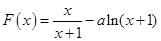 ,所以
,所以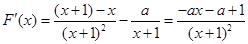 .
.
(i)当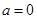 时,
时,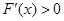 .
.
(ii)当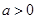 时,由
时,由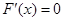 ,得到
,得到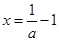 ,知在
,知在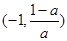 上
上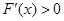 .
.
(iii)当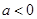 时,由
时,由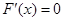 ,得到
,得到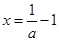 ,知在
,知在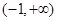 上
上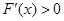 .
.
综上,当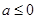 时,
时,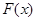 递增区间为
递增区间为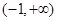 ;当
;当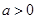 时,
时, 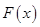 递增区间为
递增区间为 .
.
(Ⅱ)(i)因为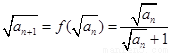 ,所以
,所以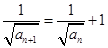 ,即
,即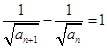 ,
,
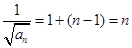 ,即
,即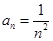 .
……………………………………(6分)
.
……………………………………(6分)
因为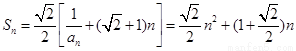 ,
,
当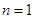 时,
时,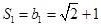 ,当
,当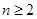 时,
时,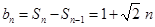 ,
,
所以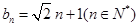 .又因为
.又因为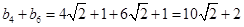 ,
,
所以令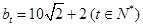 ,则
,则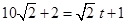
得到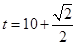 与
与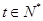 矛盾,所以
矛盾,所以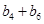 不在数列
不在数列 中. ………(9分)
中. ………(9分)
(ii)充分性:若存在整数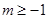 ,使
,使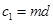 .设
.设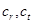 为数列
为数列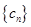 中不同的两项,则
中不同的两项,则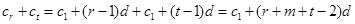
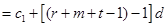 .
.
又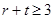 且
且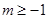 ,所以
,所以 .即
.即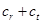 是数列
是数列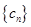 的第
的第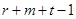 项.
项.
必要性:若数列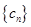 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列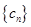 中的项,
中的项,
则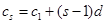 ,
,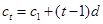 ,(
,(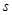 ,
,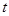 为互不相同的正整数)
为互不相同的正整数)
则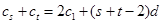 ,令
,令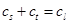 ,
,
得到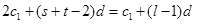
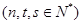 ,
,
所以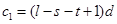 ,令整数
,令整数 ,所以
,所以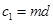 . ……(11 分)
. ……(11 分)
下证整数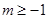 .若设整数
.若设整数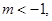 则
则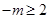 .令
.令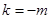 ,
,
由题设取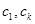 使
使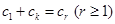
即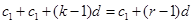 ,所以
,所以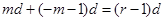
即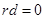 与
与 相矛盾,所以
相矛盾,所以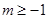 .
.
综上, 数列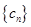 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列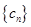 中的项的充要条件是存在整数
中的项的充要条件是存在整数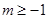 ,使
,使

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目