题目内容
已知变量a,θ∈R,则(a-2cosθ)2+(a-5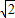 -2sinθ)2的最小值为 .
-2sinθ)2的最小值为 .
【答案】分析:设点A(a,a-5 )、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.点A在直线L:x-y-5
)、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.点A在直线L:x-y-5 =0上,点B在圆C:x2+y2=4 上,先求出圆心到直线的距离d,可得|AB|的最小值d-r,从而得到|AB|2 的最小值.
=0上,点B在圆C:x2+y2=4 上,先求出圆心到直线的距离d,可得|AB|的最小值d-r,从而得到|AB|2 的最小值.
解答:解:可设点A(a,a-5 )、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.
)、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.
由于点A在直线L:x-y-5 =0上,点B在圆C:x2+y2=4 上.
=0上,点B在圆C:x2+y2=4 上.
数形结合可知,由圆心O(0,0)向直线L作垂线,|AB|的最小值就是夹在圆与直线间的部分.
由于圆心到直线的距离d= =5,|AB|min=d-r=3,
=5,|AB|min=d-r=3,
∴|AB|2 的最小值为9,
故答案为 9.
点评:本题主要考查直线和愿的位置关系,点到直线的距离公式、两点间的距离公式的应用,属于中档题.
 )、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.点A在直线L:x-y-5
)、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.点A在直线L:x-y-5 =0上,点B在圆C:x2+y2=4 上,先求出圆心到直线的距离d,可得|AB|的最小值d-r,从而得到|AB|2 的最小值.
=0上,点B在圆C:x2+y2=4 上,先求出圆心到直线的距离d,可得|AB|的最小值d-r,从而得到|AB|2 的最小值.解答:解:可设点A(a,a-5
 )、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.
)、B(2cosθ,2sinθ),易知本题即求|AB|2 的最小值.由于点A在直线L:x-y-5
 =0上,点B在圆C:x2+y2=4 上.
=0上,点B在圆C:x2+y2=4 上.数形结合可知,由圆心O(0,0)向直线L作垂线,|AB|的最小值就是夹在圆与直线间的部分.
由于圆心到直线的距离d=
 =5,|AB|min=d-r=3,
=5,|AB|min=d-r=3,∴|AB|2 的最小值为9,
故答案为 9.
点评:本题主要考查直线和愿的位置关系,点到直线的距离公式、两点间的距离公式的应用,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 的最小值为( )
的最小值为( )