��Ŀ����
���壺���Զ�����D�ڵ���������x1��x2��x1��x2������|f��x1��-f��x2��|��|x1-x2|��������ƺ���y=f��x����D�ϵġ�ƽ����������
��1��h��x��=x2-x�Ƿ�ΪR�ϵġ�ƽ������������˵�����ɣ�
��2����֤����?k��R��f��x��=x2+kx+1���������䣨-1��1���ϵ�ƽ��������
��3��������{xn}��?n��N*�У�����|xn+1-xn|�� ����y=sinxΪ��ƽ������������֤|yn+1-y1|��1����
����y=sinxΪ��ƽ������������֤|yn+1-y1|��1����
��1���⣺ȡx1=3��x2=1����|h��x1��-h��x2��|=4��|x1-x2|�����h��x��=x2-x����R�ϵġ�ƽ����������
��2��֤�������䣨-1��1���ϵ���������x1��x2��|f��x1��-f��x2��|=|x1+x2+k||x1-x2|��
��k��0����x1��x2�ʣ� ��1��ʱ��x1+x2+k��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|��
��1��ʱ��x1+x2+k��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|��
��k��0����x1��x2�ʣ�-1��- ��ʱ��x1+x2+k��-1����|x1+x2+k|��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|��
��ʱ��x1+x2+k��-1����|x1+x2+k|��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|��
��?k��R��f��x��=x2+kx+1���������䣨-1��1���ϵ�ƽ��������
��3��֤������y=sinx��R�ϵġ�ƽ����������
��|yn+1-yn+1|��|xn+1-xn|�� ��
�� ��
�� ��
��
��|yn+1-y1|�� [��
[�� ��+��
��+��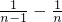 ��+��+��1-
��+��+��1- ��]=
��]= ��
��
��|yn+1-y1|��1��
��������1��ȡx1=3��x2=1����|h��x1��-h��x2��|=4��|x1-x2|�����ɵõ����ۣ�
��2�����䣨-1��1���ϵ���������x1��x2��|f��x1��-f��x2��|=|x1+x2+k||x1-x2|���������ۣ����ɵõ����ۣ�
��3������y=sinx��R�ϵġ�ƽ�����������ɵ�|yn+1-yn+1|��|xn+1-xn|�� ��
�� ��
�� ������˿ɵý��ۣ�
������˿ɵý��ۣ�
���������⿼���¶��壬����ѧ�������������������������е��⣮
��2��֤�������䣨-1��1���ϵ���������x1��x2��|f��x1��-f��x2��|=|x1+x2+k||x1-x2|��
��k��0����x1��x2�ʣ�
 ��1��ʱ��x1+x2+k��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|��
��1��ʱ��x1+x2+k��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|����k��0����x1��x2�ʣ�-1��-
 ��ʱ��x1+x2+k��-1����|x1+x2+k|��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|��
��ʱ��x1+x2+k��-1����|x1+x2+k|��1���Ӷ�|f��x1��-f��x2��|��|x1-x2|����?k��R��f��x��=x2+kx+1���������䣨-1��1���ϵ�ƽ��������
��3��֤������y=sinx��R�ϵġ�ƽ����������
��|yn+1-yn+1|��|xn+1-xn|��
 ��
�� ��
�� ��
����|yn+1-y1|��
 [��
[�� ��+��
��+��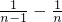 ��+��+��1-
��+��+��1- ��]=
��]= ��
��
��|yn+1-y1|��1��
��������1��ȡx1=3��x2=1����|h��x1��-h��x2��|=4��|x1-x2|�����ɵõ����ۣ�
��2�����䣨-1��1���ϵ���������x1��x2��|f��x1��-f��x2��|=|x1+x2+k||x1-x2|���������ۣ����ɵõ����ۣ�
��3������y=sinx��R�ϵġ�ƽ�����������ɵ�|yn+1-yn+1|��|xn+1-xn|��
 ��
�� ��
�� ������˿ɵý��ۣ�
������˿ɵý��ۣ����������⿼���¶��壬����ѧ�������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
 ����y=sinxΪ��ƽ������������֤|yn+1-y1|��1����
����y=sinxΪ��ƽ������������֤|yn+1-y1|��1����