题目内容
(本小题满分12分)
已知函数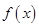 ,若
,若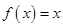 ,则称
,则称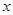 为
为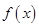 的“不动点”;若
的“不动点”;若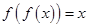 ,则称
,则称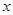 为
为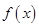 的“稳定点”。记集合
的“稳定点”。记集合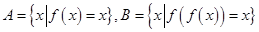
(1)已知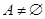 ,若
,若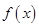 是在
是在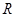 上单调递增函数,是否有
上单调递增函数,是否有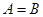 ?若是,请证明。
?若是,请证明。
(2)记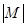 表示集合
表示集合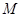 中元素的个数,问:
中元素的个数,问:
 若函数
若函数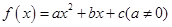 ,若
,若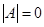 ,则
,则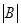 是否等于0?若是,请证明
是否等于0?若是,请证明
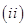 若
若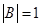 ,试问:
,试问: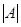 是否一定等于1?若是,请证明
是否一定等于1?若是,请证明
已知函数
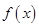 ,若
,若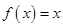 ,则称
,则称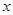 为
为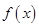 的“不动点”;若
的“不动点”;若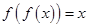 ,则称
,则称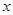 为
为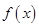 的“稳定点”。记集合
的“稳定点”。记集合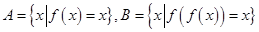
(1)已知
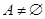 ,若
,若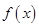 是在
是在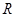 上单调递增函数,是否有
上单调递增函数,是否有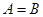 ?若是,请证明。
?若是,请证明。(2)记
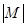 表示集合
表示集合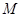 中元素的个数,问:
中元素的个数,问: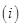 若函数
若函数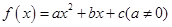 ,若
,若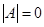 ,则
,则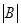 是否等于0?若是,请证明
是否等于0?若是,请证明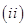 若
若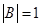 ,试问:
,试问: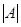 是否一定等于1?若是,请证明
是否一定等于1?若是,请证明(1)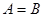 (2)
(2)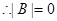 ,
,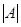 是不一定等于1。
是不一定等于1。
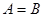 (2)
(2)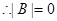 ,
,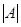 是不一定等于1。
是不一定等于1。试题分析:(1)证明:先证 任取
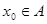 ,则
,则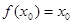

再证 任取
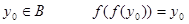
若
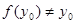 ,不妨设
,不妨设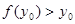
由单调递增可知:
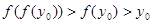 与
与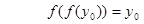 矛盾
矛盾同理
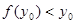 也矛盾,所以
也矛盾,所以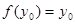
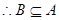
综上:
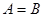
(2)①若
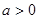 由于
由于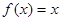 无实根 则对任意实数x,
无实根 则对任意实数x,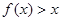
从而
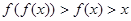 故
故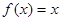 无实根
无实根同理若
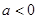 对任意实数x,
对任意实数x, 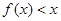 ,从而
,从而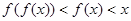
故
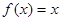 也无实根
也无实根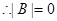
②不妨设
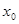 是B中唯一元素 则
是B中唯一元素 则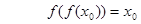
令
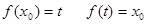 那么
那么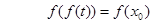 而
而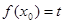
故

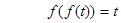 说明t也是
说明t也是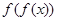 的不动点
的不动点由于
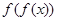 只有唯一的不动点 故
只有唯一的不动点 故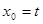 即
即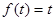
这说明t也是
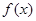 的不动点,从而存在性得证
的不动点,从而存在性得证以下证明唯一性:若
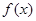 还有另外一个不动点m,即
还有另外一个不动点m,即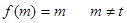
则
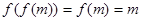 这说明
这说明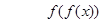
 还有另外一个稳定点m
还有另外一个稳定点m与题设矛盾。
点评:结合新定义,和已学的函数单调性的性质,来分析函数的最值, 同时对于不动点的问题,要加以转化为方程根的问题来处理,属于中档题。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
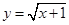 的定义域为集合
的定义域为集合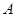 ,不等式
,不等式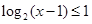 的解集为集合
的解集为集合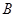 .
.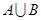 ,
,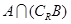 .
. ,集合
,集合 ,则
,则

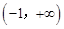


 和
和 ,定义
,定义 ,
,

 ,设
,设 ,
, ,则
,则



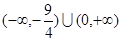
 ,
, ,则
,则 等于
等于



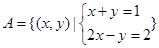 表示同一集合的是
表示同一集合的是



 ,B=
,B= ,且A="B" ,则实数
,且A="B" ,则实数 。
。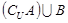 为
为