题目内容
如下图，在半径为1的半圆内，放置一个边长为
的正方形ABCD，向半圆内任投一点，该点落在正方形内的概率是
- A.π
- B.
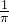
- C.
- D.2π
C
分析：先明确是几何概型中的面积类型，再分别求出半圆与正方形的面积，进而由概率公式求得要应面积的比值即可得到答案．
解答：根据题意可得此问题是几何概型，
因为半圆的半径为1，所以其面积为：
；
因为正方形的边长为，所以其面积为
；
所以该点落在正方形内的概率为：
，．
故选C．
点评：本题主要考查几何概型中的面积类型，方法是分别求相应面积，再求其比值．
分析：先明确是几何概型中的面积类型，再分别求出半圆与正方形的面积，进而由概率公式求得要应面积的比值即可得到答案．
解答：根据题意可得此问题是几何概型，
因为半圆的半径为1，所以其面积为：
；因为正方形的边长为
，所以其面积为；所以该点落在正方形内的概率为：
，．故选C．
点评：本题主要考查几何概型中的面积类型，方法是分别求相应面积，再求其比值．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如下图，在半径为1的半圆内，放置一个边长为
的正方形ABCD，向半圆内任投一点，该点落在正方形内的概率为_________.
的正方形ABCD，向半圆内任投一点，该点落在正方形内的概率是（ ）
的正方 形ABCD， 若向半圆内任意投一点，则该点落在正方形内的概率为 ▲ 。 