题目内容
等差数列{an}的前n项和记为Sn.已知a10=30,a20=50.(Ⅰ)求通项an;
(Ⅱ)若Sn=242,求n.
【答案】分析:(1)利用等差数列的通项公式,根据a10和a20的值建立方程组,求得a1和d,则通项an可得.
(2)把等差数列的求和公式代入Sn=242进而求得n.
解答:解:(Ⅰ)由an=a1+(n-1)d,a10=30,a20=50,得
方程组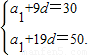
解得a1=12,d=2.所以an=2n+10.
(Ⅱ)由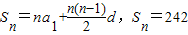 得
得
方程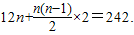
解得n=11或n=-22(舍去).
点评:本小题主要考查等差数列的通项公式、求和公式,考查运算能力.
(2)把等差数列的求和公式代入Sn=242进而求得n.
解答:解:(Ⅰ)由an=a1+(n-1)d,a10=30,a20=50,得
方程组
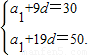
解得a1=12,d=2.所以an=2n+10.
(Ⅱ)由
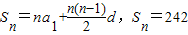 得
得方程
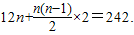
解得n=11或n=-22(舍去).
点评:本小题主要考查等差数列的通项公式、求和公式,考查运算能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |