题目内容
已知双曲线
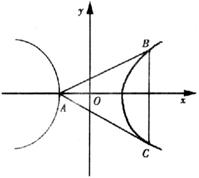
=1(a＞0，b＞0)的左顶点为A(-1，0)，过点A作两条直线分别交双曲线的右支于B(x1，y1)、C(x2，y2)两点，且△ABC为正三角形． (Ⅰ)证明：B、C两点关于x轴对称；
(Ⅱ)设x1＞2，求b的取值范围．
(1)证：∵|AB|=|AC|
∴(x1+1)2+
=(x2+1)2+
．
∵a=1 ∴
=1
∴(x1+1)2+b2(
-1)=(x2+1)2+b2(
-1)
整理，得(x1-x2)[(xl+x2)(1+b2)+2]=0
∵x1＞0，x2＞0 ∴(xl+x2)(1+b2)+2＞0
∴x1=x2(5分)
∴BC⊥x轴，根据双曲线的对称性，B、C关于x轴对称
(Ⅱ)解：(法一)根据(Ⅰ)及∠A=60°，设AB的方程为y=
(x+1)
代入x2-
=1并整理，得(3b2-1)x2-2x-(3b2+1)=0
∵-1，x1是方程的两根，且x1＞2
∴3b2-1＞0，且-1·x1=
∴
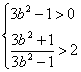解得
＜b2＜l
∵b＞0，∴b的取值范围为(
，1)
(法二)根据(1)及∠A=60°，得y1=
(x1+1)
∵B(xl，y1)在双曲线x2-
=1上，
∴
=1
整理得b2=
∵x1＞2,∴0＜1+
＜3, ∴
＜b2＜1
∵b＞0,∴
＜b＜1, ∴b的范围是（
，1）.
练习册系列答案
相关题目
=1(a＞0,b＞0)的动弦BC平行于虚轴，M、N是双曲线的左、右顶点,
=1(a＞0,b＞0)的离心率e∈［
,2］，令双曲线两条渐近线构成的角中，以实轴为角平分线的角为θ,则θ的取值范围是( )
］ B.［
］
］ D.［
,π］
=1(a＞0，b＞0)的右焦点为F，若过F且倾斜角为60°的直线与双曲线有且只有一个交点，则双曲线的离心率是( )
B．
C．4 D．2
=1(a＞0,b＞0)的一条渐近线为y=kx(k＞0),离心率e=
k,则双曲线方程为( )
=1 B.
=1
=1 D.
=1
=1(a>0,b>0)的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
(O为原点),则两条渐近线的夹角为( )