题目内容
用数学归纳法证明：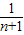
+
+
+…+
＞
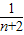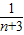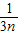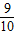（n＞1，且n∈N*）．
【答案】分析：先证明n=2时，结论成立；假设n=k（k＞1，且k∈N*）时结论成立，利用归纳假设，证明n=k+1时结论成立．
解答：证明：（1）n=2时，左边=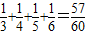
＞
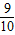，不等式成立；
（2）假设n=k（k＞1，且k∈N*）时结论成立，即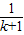
+
+…+
＞
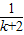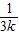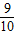
则n=k+1时，左边=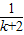
+
+…+
+
=
+
+…+
+
-
＞
+
-
=
＞
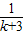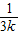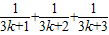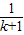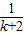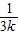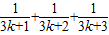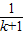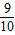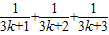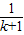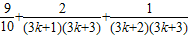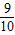
即n=k+1时结论成立
综上，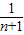
+
+
+…+
＞
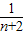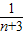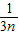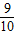（n＞1，且n∈N*）．
点评：本题考查数学归纳法，考查不等式的证明，掌握数学归纳法的证题步骤是关键．
解答：证明：（1）n=2时，左边=
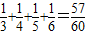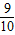＞，不等式成立；（2）假设n=k（k＞1，且k∈N*）时结论成立，即
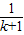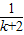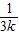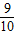
++…+＞则n=k+1时，左边=
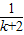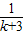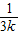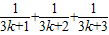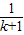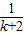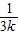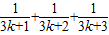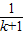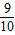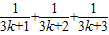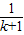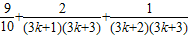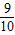
++…++=++…++-＞+-=＞即n=k+1时结论成立
综上，
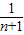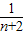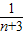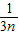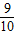+++…+＞（n＞1，且n∈N*）．点评：本题考查数学归纳法，考查不等式的证明，掌握数学归纳法的证题步骤是关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目