Question

（本小题满分12分）如图，直三棱柱中，、分别为、的中点，平面            

（I）证明：

（II）设二面角为60°，求与平面所成的角的大小。

Answer 1

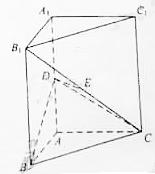
解析：（I）分析一：连结BE，为直三棱柱，

为的中点，。又平面，

（射影相等的两条斜线段相等）而平面，

（相等的斜线段的射影相等）。

分析二：取的中点，证四边形为平行四边形，进而证∥，，得也可。

分析三：利用空间向量的方法。具体解析法略。

（II）分析一：求与平面所成的线面角，只需求点到面的距离即可。

作于，连，则，为二面角的平面角，.不妨设，则.在中，由，易得.

   设点到面的距离为，与平面所成的角为。利用，可求得，又可求得 

即与平面所成的角为

分析二：作出与平面所成的角再行求解析。如图可证得，所以面。由分析一易知：四边形为正方形，连，并设交点为，则，为在面内的射影。。以下略。

分析三：利用空间向量的方法求出面的法向量，则与平面所成的角即为与法向量的夹角的余角。具体解析法详见高考试题参考答案。

总之在目前，立体几何中的两种主要的处理方法：传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会兼顾双方的利益。