题目内容
如图,P是正方形ABCD所在平面外一点,且PA⊥平面ABCD,AE⊥PD,EF∥CD,AM=EF.
(1)证明MF是异面直线AB与PC的公垂线;
(2)若PA=3AB,求直线AC与平面AEM所成角的正弦值.
(1)证明:∵EF∥CD,CD∥AM,
∴EF∥AM.
又AM=EF,
∴四边形AEFM为平行四边形.
∵PA⊥平面ABCD,
∴PA⊥AM.而AM⊥AD,
∴AM⊥平面PAD.从而AM⊥AE.
∴四边形AEFM为矩形.
∴MF⊥AB于M.
又AE⊥PD,AE⊥EF,
∴AE⊥平面PDC.从而MF⊥平面PDC.
∴MF⊥PC于F,因此命题成立.
(2)解:如下图,连结BD交AC于O,连结BE,过O作BE的垂线OH,垂足为H.
依题意,PD⊥平面AEM,
∴ED⊥BE.

又OH⊥BE,
∴OH∥DE.
因此OH⊥平面AEM.连结AH,则∠HAO是直线AC与平面AEM所成的角.
设AB=a,则PA=![]() AC=
AC=![]() ,
,
由Rt△ADE∽Rt△PDA,得ED=![]() ,OH=
,OH=![]() ED=
ED=![]() ,
,
∴sin∠HAO=![]() ,
,
即AC与平面AEM所成角的正弦值为![]() .
.

练习册系列答案
相关题目
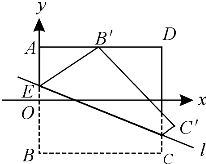 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式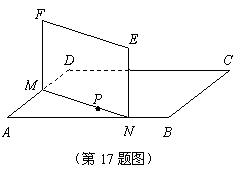 (2)求S关于x的函数关系式及该函数的定义域;
(2)求S关于x的函数关系式及该函数的定义域;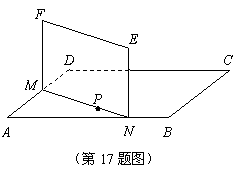 (2)求S关于x的函数关系式及该函数的定义域;
(2)求S关于x的函数关系式及该函数的定义域; (1) 用x的代数式表示AM;(2)求S关于x的函数关系式及该函数的定义域;
(1) 用x的代数式表示AM;(2)求S关于x的函数关系式及该函数的定义域;