题目内容
(本小题满分12分)
在正四棱锥V - ABCD中,P,Q分别为棱VB,VD的中点, 点M在边BC上,且BM: BC = 1 : 3,AB =2 ,VA =" 6."
,VA =" 6." 
(I )求证CQ∥平面PAN;
(II)求证:CQ⊥AP.
(I )只需证平面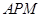 ∥平面
∥平面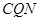 ;(II)只需证
;(II)只需证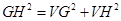 。
。
解析试题分析:(Ⅰ)连接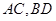 ,设
,设 ,则
,则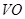 ⊥平面
⊥平面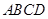 ,
,
连接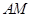 ,设
,设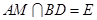 ,由
,由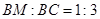 ,
,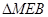 ~
~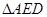 ,
,
得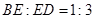 ∴
∴ 为
为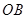 的中点,而
的中点,而 为
为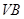 的中点,故
的中点,故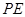 ∥
∥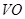
在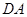 上取一点
上取一点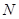 ,使
,使 ,
,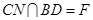 同理
同理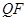 ∥
∥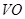 ,于是
,于是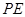 ∥
∥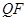
在正方形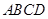 中
中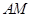 ∥
∥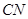 ,∴平面
,∴平面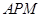 ∥平面
∥平面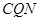 ,又
,又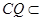 平面
平面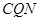
∴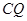 ∥平面
∥平面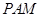 ; …6分
; …6分
(Ⅱ)延长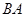 至
至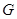 使
使 ,连接
,连接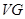 ,则
,则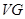 ∥
∥ 且
且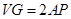
延长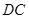 至
至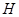 使
使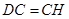 ,连接
,连接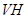 ,,则
,,则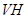 ∥
∥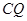 且
且
∴相交直线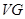 与
与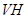 所成的不大于
所成的不大于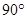 的角即为异面直线
的角即为异面直线 与
与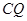 所成的角
所成的角
连接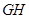 ,在
,在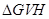 中,
中,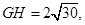
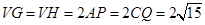
∴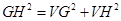 ,∴
,∴ ,即
,即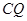 ⊥
⊥ . …12分
. …12分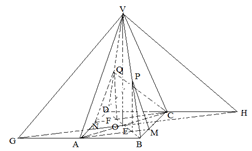
考点:线面平行的判断;先线垂直的判断;正四棱锥的结构特征。
点评:①本题主要考查了空间的线面平行,线线垂直的证明,充分考查了学生的逻辑推理能力,空间想象力,以及识图能力。②我们要熟练掌握正棱柱、直棱柱、正棱锥的结构特征。正棱柱:底面是正多边形,侧棱垂直底面;直棱柱:侧棱垂直底面;正棱锥:底面是正多边形,顶点在底面的投影是底面的中心。

练习册系列答案
相关题目
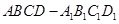 是棱长为1的正方体,四棱锥
是棱长为1的正方体,四棱锥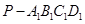 中,
中,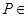 平面
平面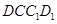 ,
,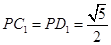 。
。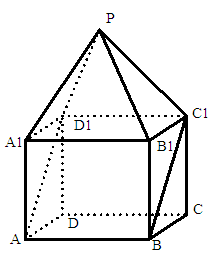
 与平面
与平面 所成角的正切值。
所成角的正切值。
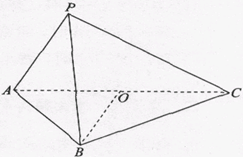
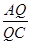 的值;若不存在,说明理由。
的值;若不存在,说明理由。 BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.
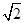 ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。
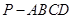 中,底面
中,底面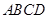 是矩形,
是矩形,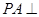 平面
平面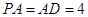 ,
,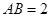 .
.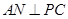 于点
于点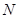 ,
, 是
是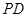 中点.
中点.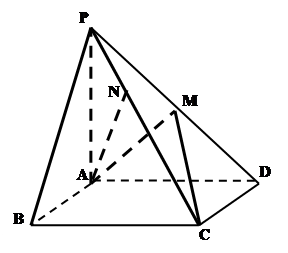
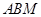 ⊥平面
⊥平面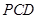 ;
; 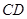 与平面
与平面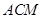 所成的角的正弦值;
所成的角的正弦值;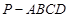 中,底面
中,底面 为矩形,
为矩形,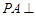 平面
平面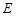 在线段
在线段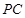 上,
上,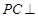 平面
平面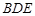 .
.
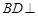 平面
平面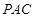 ;
;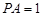 ,
,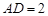 ,求二面角
,求二面角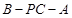 的正切值.
的正切值.