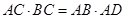��Ŀ����
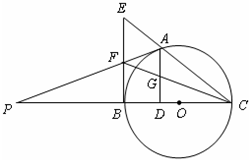
��ѡ��4-1����ͼ���ڡ�ABC�У���ABC=90°����BCΪֱ����ԲO��AC�ڵ�D����EΪAB���е㣮��I����֤��ֱ��DEΪԲO�����ߣ�
������CE��ԲO�ڵ�F����֤��CD•CA=CF•CE
��ѡ��4-4����ƽ��ֱ������ϵxoy�У�ԲC�IJ�������Ϊ
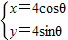 ����Ϊ��������ֱ��l������p��2��2������б��a=
����Ϊ��������ֱ��l������p��2��2������б��a=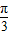 ��
����I��д��ԲC�ı����̺�ֱ��l�IJ������̣�
������ֱ��l��ԲC�ཻ��A��B���㣬��|PA|-|PB|��ֵ��
��ѡ��4-5����֪����f��x��=|2x+1|��g��x��=|x|+a
����a=0ʱ���ⲻ��ʽf��x����g��x����
����������x��R��ʹ��f��x����g��x����������ʵ��a��ȡֵ��Χ��
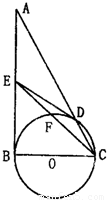
���𰸡���������ѡ��4-1�������������������������ε�������á�EDO=��EDB+��ODB=��EBD+��OBD=90°���ɵ�ֱ��DEΪԲO�����ߣ�
��������DF�����С�DFC=��DBC��֤�� D��A��E��F�ĵ㹲Բ���ɵ� CD•CA=CF•CE��
��ѡ��4-4������Բ�IJ�����������ͬ�����Ǻ����Ļ�����ϵ��ȥ��������Ϊ�����̣���ֱ��l�IJ���������ȥ��������Ϊֱ�����귽�̣�
����ֱ�ߵķ��̴���Բ�ķ��̣����ø���ϵ���Ĺ�ϵ�Լ������ļ����������|PA|•|PB|��ֵ��
��ѡ��4-5������ a=0 ʱ����f��x����g��x�� ��|2x+1|��x������ƽ�������� 3x2+4x+1��0�����һԪ���β���ʽ���x�ķ�Χ����Ϊ����
������ f��x����g��x�� �� a��|2x+1|-|x|����h��x��=|2x+1|-|x|����� h��x������Сֵ���������ʵ��a��ȡֵ��Χ��
�����ѡ��4-1������֤��������BD��OD����Rt��ABD�У�DE= =BE�����ڵ���������EBD�У���EBD=��EDB��
=BE�����ڵ���������EBD�У���EBD=��EDB��
�ڵ���������OBD�У���OBD=��ODB���ɵá�EDO=��EDB+��ODB=��EBD+��OBD=90°��
��ֱ��DEΪԲO�����ߣ�

��������DF������DFC=��DBC��
����Ϊ��A=��DBC���ɵá�A=��DFC������ D��A��E��F�ĵ㹲Բ��
��˵õ�CD•CA=CF•CE��
��ѡ��4-4���⣺����Բ�ı�����Ϊ x2+y2=16��
ֱ��l�IJ�������Ϊ ����
����  ��t��������
��t��������
����ֱ�ߵķ��� ���� x2+y2=16��
���� x2+y2=16��
�� +
+ =16��t2+2��
=16��t2+2�� +1��t-8=0��
+1��t-8=0��
���� t1•t2=-8����|PA|•|PB|=8��
��ѡ��4-5���⣺���� a=0 ʱ����f��x����g��x�� ��|2x+1|��x��
����ƽ�������� 3x2+4x+1��0��
��֮��x��-1���� x��- ����ԭ����ʽ�Ľ⼯Ϊ��-�ޣ�-1]��[-
����ԭ����ʽ�Ľ⼯Ϊ��-�ޣ�-1]��[- ��+�ޣ���
��+�ޣ���
������ f��x����g��x�� �� a��|2x+1|-|x|��
��h��x��=|2x+1|-|x|���� h��x��= ����h��x�� ����СֵΪh��-
����h��x�� ����СֵΪh��- ��=-
��=- ��
��
�Ӷ�����ʵ�� a�ķ�ΧΪ[- ��+�ޣ���
��+�ޣ���
������������Ҫ����Բ�IJ������̡�Բ�����߷��̡���Բ�йصı����߶Σ�����ֵ����ʽ�Ľⷨ�������е��⣮
��������DF�����С�DFC=��DBC��֤�� D��A��E��F�ĵ㹲Բ���ɵ� CD•CA=CF•CE��
��ѡ��4-4������Բ�IJ�����������ͬ�����Ǻ����Ļ�����ϵ��ȥ��������Ϊ�����̣���ֱ��l�IJ���������ȥ��������Ϊֱ�����귽�̣�
����ֱ�ߵķ��̴���Բ�ķ��̣����ø���ϵ���Ĺ�ϵ�Լ������ļ����������|PA|•|PB|��ֵ��
��ѡ��4-5������ a=0 ʱ����f��x����g��x�� ��|2x+1|��x������ƽ�������� 3x2+4x+1��0�����һԪ���β���ʽ���x�ķ�Χ����Ϊ����
������ f��x����g��x�� �� a��|2x+1|-|x|����h��x��=|2x+1|-|x|����� h��x������Сֵ���������ʵ��a��ȡֵ��Χ��
�����ѡ��4-1������֤��������BD��OD����Rt��ABD�У�DE=
 =BE�����ڵ���������EBD�У���EBD=��EDB��
=BE�����ڵ���������EBD�У���EBD=��EDB���ڵ���������OBD�У���OBD=��ODB���ɵá�EDO=��EDB+��ODB=��EBD+��OBD=90°��
��ֱ��DEΪԲO�����ߣ�

��������DF������DFC=��DBC��
����Ϊ��A=��DBC���ɵá�A=��DFC������ D��A��E��F�ĵ㹲Բ��
��˵õ�CD•CA=CF•CE��
��ѡ��4-4���⣺����Բ�ı�����Ϊ x2+y2=16��
ֱ��l�IJ�������Ϊ
 ����
����  ��t��������
��tΪ������������ֱ�ߵķ���
 ���� x2+y2=16��
���� x2+y2=16����
 +
+ =16��t2+2��
=16��t2+2�� +1��t-8=0��
+1��t-8=0������ t1•t2=-8����|PA|•|PB|=8��
��ѡ��4-5���⣺���� a=0 ʱ����f��x����g��x�� ��|2x+1|��x��
����ƽ�������� 3x2+4x+1��0��
��֮��x��-1���� x��-
 ����ԭ����ʽ�Ľ⼯Ϊ��-�ޣ�-1]��[-
����ԭ����ʽ�Ľ⼯Ϊ��-�ޣ�-1]��[- ��+�ޣ���
��+�ޣ��������� f��x����g��x�� �� a��|2x+1|-|x|��
��h��x��=|2x+1|-|x|���� h��x��=
 ����h��x�� ����СֵΪh��-
����h��x�� ����СֵΪh��- ��=-
��=- ��
���Ӷ�����ʵ�� a�ķ�ΧΪ[-
 ��+�ޣ���
��+�ޣ���������������Ҫ����Բ�IJ������̡�Բ�����߷��̡���Բ�йصı����߶Σ�����ֵ����ʽ�Ľⷨ�������е��⣮

��ϰ��ϵ�д�
�����Ŀ
 ѡ��4-1��
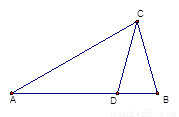
ѡ��4-1�� ��ѡ��4-1����ͼ������ACD����ABC��������ʽ���г������ǣ�������
��ѡ��4-1����ͼ������ACD����ABC��������ʽ���г������ǣ�������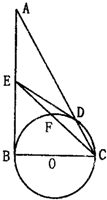 ��ѡ��4-1����ͼ���ڡ�ABC�У���ABC=90�㣬��BCΪֱ����ԲO��AC�ڵ�D����EΪAB���е㣮
��ѡ��4-1����ͼ���ڡ�ABC�У���ABC=90�㣬��BCΪֱ����ԲO��AC�ڵ�D����EΪAB���е㣮  ��PC��1����ԲO�İ뾶Ϊ________ ��
��PC��1����ԲO�İ뾶Ϊ________ ��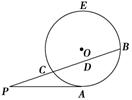
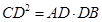 B��
B��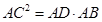
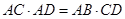 D��
D��