题目内容
(本题满分12分)设抛物线C
：y=x
-2x+2与抛物线C
：y=-x+ax+b在它们的一个交点处的切线互相垂直.(1)求a、b之间的关系；(2)若a>0,b>0,求ab的最大值.
(Ⅰ) a+b=
(Ⅱ) 
解析:
：（1）设两抛物线的交点为M（x0,y0）,由题意知x
-2x
+2=-x+ax+b,整理得2x-(2+a)x+2-b=0 ①由导数可得抛物线C
、C
在交点M处的切线斜率为k=2x-2,k=-2x+a,因两切线互相垂直，则有kk=-1,即(2x-2)(-2x+a)=-1.整理得2［2x-(2+a)x］+2a-1=0 ②,联立①和②，消去x得:a+b=.
(2)由（1）知a+b=,又a>0,b>0,∴ab≤(
)
=
=.当且仅当，a=b=
时取等号，
故ab的最大值为.
练习册系列答案
相关题目
:实数
满足
, 命题
:实数
.
为真，求实数
.
的单调区间；
对
恒成立，求实数
的取值范围.
,其中
。
时，求不等式
的解集；
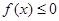的解集为
，求a的值。
与
垂直，求
的值 
的最大值; 
,
分别是椭圆
：
的左、右焦点，过
与
、
两点，且
，
，
成等差数列，
满足
,求