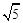题目内容
设F是抛物线C:y2=4x的焦点,过点A(-1,0)的直线l与抛物线C相交于M、N两点.(Ⅰ)求线段MN的中点轨迹方程;
(Ⅱ)若![]() ,求λ的取值范围.
,求λ的取值范围.
解:设l的方程为 y=k(x+1)
由
得k2x2+(2k2-4)x+k2=0
因为l与C有两个不同的交点,所以

解之得-1<k<1,且k≠0.
(Ⅰ)设M(x1,y1)、N(x2,y2),则
x1+x2=![]() ,x1x2=1
,x1x2=1
设MN的中点P(x,y),则x![]()
又y=k(x+1) 消去k得y2=2(x+1)
∵-1<k<1,且k≠0,∴x![]()
∴MN的中点P(x,y)的轨迹方程为y2=2(x+1)(x>1)
(Ⅱ)由![]() =λ
=λ![]() ,知(x1+1,y1)=λ(x2+1,y2)
,知(x1+1,y1)=λ(x2+1,y2)
∴
由②得![]() 即4x1=λ2·4x2 ∴x1=λ2x2 ③
即4x1=λ2·4x2 ∴x1=λ2x2 ③
由①,③得λ(λ-1)x2=λ-1
∵M与N不同 ∴λ≠1
∴x2=![]() ,x1=λ
,x1=λ
于是λ+![]() .
.
∵0<k2<1 ∴![]() >1;
>1;![]() -2>2
-2>2
∴λ+![]() >2 ∴λ>0且λ≠1
>2 ∴λ>0且λ≠1
即λ的取值范围为(0,1)∪(1,+∞).

练习册系列答案
相关题目
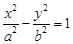
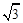 (C)
(C)
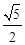 (D)
(D) 
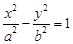
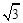 (C)
(C)
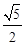 (D)
(D)