题目内容
(本小题满分16分)如图,在平面直角坐标系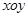 中,已知
中,已知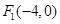 ,
,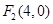 ,
,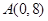 ,直线
,直线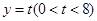 与线段
与线段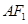 、
、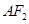 分别交于点
分别交于点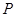 、
、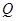 .
.
(Ⅰ)当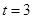 时,求以
时,求以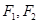 为焦点,且过
为焦点,且过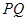 中点的椭圆的标准方程;
中点的椭圆的标准方程;
(Ⅱ)过点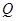 作直线
作直线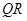 ∥
∥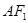 交
交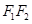 于点
于点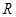 ,记
,记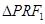 的外接圆为圆
的外接圆为圆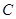 .
.
① 求证:圆心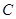 在定直线
在定直线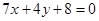 上;
上;
② 圆 是否恒过异于点
是否恒过异于点 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由.
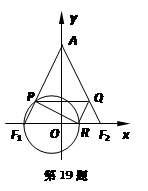
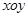 中,已知
中,已知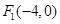 ,
,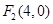 ,
,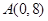 ,直线
,直线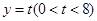 与线段
与线段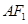 、
、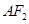 分别交于点
分别交于点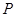 、
、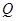 .
.(Ⅰ)当
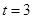 时,求以
时,求以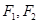 为焦点,且过
为焦点,且过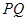 中点的椭圆的标准方程;
中点的椭圆的标准方程;(Ⅱ)过点
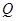 作直线
作直线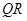 ∥
∥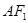 交
交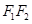 于点
于点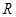 ,记
,记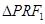 的外接圆为圆
的外接圆为圆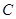 .
.① 求证:圆心
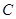 在定直线
在定直线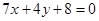 上;
上;② 圆
 是否恒过异于点
是否恒过异于点 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由. 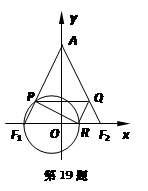
(Ⅰ)设椭圆的方程为 ,当
,当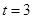 时,PQ的中点为(0,3),所以b=3……………3分
时,PQ的中点为(0,3),所以b=3……………3分
而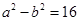 ,所以
,所以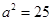 ,故椭圆的标准方程为
,故椭圆的标准方程为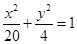 …………………5分
…………………5分
(Ⅱ)①解法一:易得直线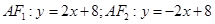 ,
,
所以可得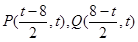 ,再由
,再由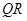 ∥
∥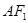 ,得
,得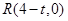 ……………8分
……………8分
则线段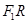 的中垂线方程为
的中垂线方程为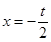 , 线段
, 线段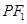 的中垂线方程为
的中垂线方程为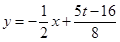 ,
,
由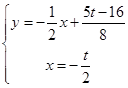 ,解得
,解得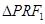 的外接圆的圆心坐标为
的外接圆的圆心坐标为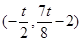 ………10分
………10分
经验证,该圆心在定直线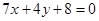 上…………………………… 11分
上…………………………… 11分
解法二: 易得直线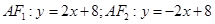 ,所以可得
,所以可得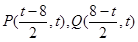 ,再由
,再由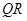 ∥
∥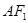 ,得
,得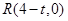 ………………………8分
………………………8分
设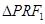 的外接圆
的外接圆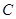 的方程为
的方程为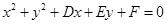 ,
,
则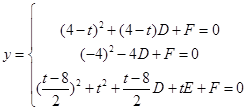 ,解得
,解得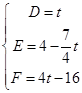 …10分
…10分
所以圆心坐标为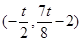 ,经验证,该圆心在定直线
,经验证,该圆心在定直线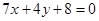 上 …11分
上 …11分
②由①可得圆C的方程为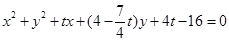 ………13分
………13分
该方程可整理为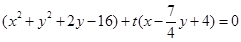 ,
,
则由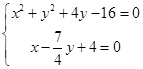 ,解得
,解得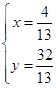 或
或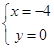 ,
,
所以圆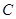 恒过异于点
恒过异于点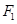 的一个定点,该点坐标为
的一个定点,该点坐标为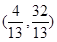 ………………16分
………………16分
 ,当
,当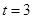 时,PQ的中点为(0,3),所以b=3……………3分
时,PQ的中点为(0,3),所以b=3……………3分 而
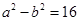 ,所以
,所以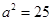 ,故椭圆的标准方程为
,故椭圆的标准方程为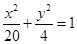 …………………5分
…………………5分(Ⅱ)①解法一:易得直线
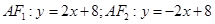 ,
,所以可得
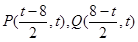 ,再由
,再由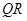 ∥
∥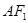 ,得
,得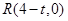 ……………8分
……………8分则线段
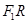 的中垂线方程为
的中垂线方程为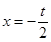 , 线段
, 线段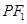 的中垂线方程为
的中垂线方程为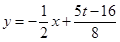 ,
,由
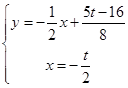 ,解得
,解得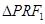 的外接圆的圆心坐标为
的外接圆的圆心坐标为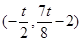 ………10分
………10分经验证,该圆心在定直线
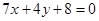 上…………………………… 11分
上…………………………… 11分解法二: 易得直线
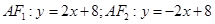 ,所以可得
,所以可得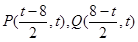 ,再由
,再由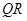 ∥
∥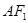 ,得
,得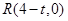 ………………………8分
………………………8分设
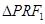 的外接圆
的外接圆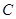 的方程为
的方程为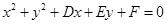 ,
,则
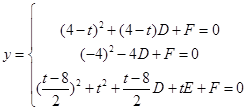 ,解得
,解得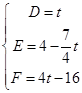 …10分
…10分所以圆心坐标为
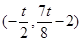 ,经验证,该圆心在定直线
,经验证,该圆心在定直线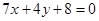 上 …11分
上 …11分②由①可得圆C的方程为
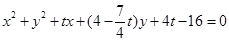 ………13分
………13分该方程可整理为
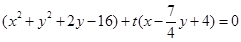 ,
,则由
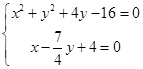 ,解得
,解得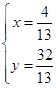 或
或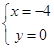 ,
,所以圆
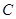 恒过异于点
恒过异于点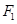 的一个定点,该点坐标为
的一个定点,该点坐标为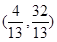 ………………16分
………………16分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的两条切线,设切点分别为P、Q,则线段PQ的长为——
的两条切线,设切点分别为P、Q,则线段PQ的长为—— 与圆
与圆 相交于
相交于 两点,且
两点,且 (其中
(其中 为原点),则
为原点),则 的值为( )
的值为( ) 或
或
 或
或
 关于直线
关于直线 对称的圆的方程是
对称的圆的方程是 ,则实数
,则实数 的值是
的值是  B = 90°,AC = 4,BC =
B = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以 为圆心,1为半径作
为圆心,1为半径作 .
.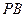 ,若
,若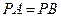 ,试判断
,试判断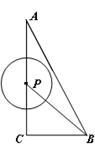
 -4
-4 -4+
-4+ =0的圆心是点P,则点P到直线
=0的圆心是点P,则点P到直线 -1=0的距离是 .
-1=0的距离是 . 内的点
内的点 的最长弦和最短弦分别为
的最长弦和最短弦分别为 和
和 ,则四边形
,则四边形 的面积等于 .
的面积等于 . 为圆
为圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与该圆的位置关系为
与该圆的位置关系为 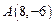 与圆
与圆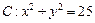 ,
,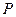 是圆
是圆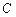 上任意一点,则
上任意一点,则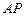 的最小值
的最小值