题目内容
(本小题满分13分)
已知圆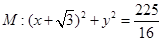 的圆心为
的圆心为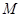 ,圆
,圆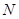 :
: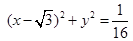 的圆心为
的圆心为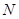 ,一动圆与圆
,一动圆与圆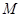 内切,与圆
内切,与圆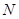 外切.
外切.
(Ⅰ)求动圆圆心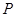 的轨迹方程;
的轨迹方程;
(Ⅱ)在(Ⅰ)所求轨迹上是否存在一点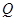 ,使得
,使得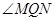 为钝角?若存在,求出点
为钝角?若存在,求出点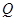 横坐标的取值范围;若不存在,说明理由.
横坐标的取值范围;若不存在,说明理由.
【答案】
解: (Ⅰ)设动圆P的半径为r,则
两式相加得|PM|+|PN|=4>|MN|
由椭圆定义知,点P的轨迹是以M、N为焦点,焦距为 ,实轴长为4的椭圆
,实轴长为4的椭圆
其方程为 …………………………………………………………6分
…………………………………………………………6分
(Ⅱ)假设存在,设 (x,y).则因为
(x,y).则因为 为钝角,所以
为钝角,所以
 ,
, ,
,
又因为 点在椭圆上,所以
点在椭圆上,所以
联立两式得: 化简得:
化简得: ,
,
解得: ,所以存在。………………………………………………… 13分
,所以存在。………………………………………………… 13分
【解析】

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和