题目内容
【题目】已知函数![]() ,
,![]() 的图象经过
的图象经过![]() 和
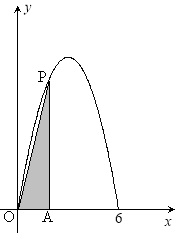
和![]() 两点,如图所示,且函数
两点,如图所示,且函数![]() 的值域为
的值域为![]() .过该函数图象上的动点
.过该函数图象上的动点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
(I)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(I)![]() ;(II)三角形面积的最大值为16.
;(II)三角形面积的最大值为16.
【解析】
试题分析:(I)用待定系数法.由抛物线的对称性及题设可知,函数![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() .
.
将顶点坐标及点(0,0),(0,6)的坐标代入解析式得关于a,b,c方程组,解此方程组,便可得 ![]() 的解析式.
的解析式.
(II)用三角形面积公式求得三角形的面积与t之间的函数关系式,然后利用导数可求得![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
试题解析:(I)由已知可得函数![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() . 2分
. 2分
方法一:由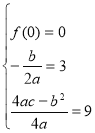
得![]() 5分
5分
得![]() 6分
6分
方法二:设![]() 4分
4分
由![]() ,得
,得![]() 5分
5分
![]() 6分
6分
(II)![]() 8分
8分
![]() 9分
9分
列表得:
|
| 4 |
|
| + | 0 | - |
|
| 极大值 |
|
11分
由上表可得![]() 时,三角形面积取得最大值
时,三角形面积取得最大值
即![]() 13分
13分

练习册系列答案
相关题目
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: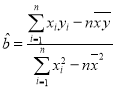 ,
,![]() ,
,![]() ,
,![]() .
.