题目内容
已知函数f（x）=asinx﹣x+b（a，b均为正常数）．
（1）若a=2，求函数f（x）在区间[0，π]上的单调减区间；
（2）设函数在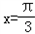
处有极值．
①对于一切
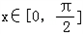，不等式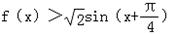
恒成立，求b的取值范围；
②若函数f（x）在区间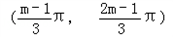
上是单调增函数，求实数m的取值范围．
（1）若a=2，求函数f（x）在区间[0，π]上的单调减区间；
（2）设函数在
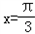处有极值．①对于一切
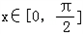，不等式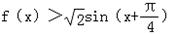恒成立，求b的取值范围；②若函数f（x）在区间
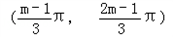上是单调增函数，求实数m的取值范围．解：（1）a=2时，函数f（x）=2sinx﹣x+b，
求导函数可得：f'（x）=2cosx﹣1
令f'（x）＜0，可得cosx＜
∵x∈[0，π]，
∴
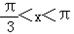
∴函数的单调减区间为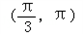
（2）f'（x）=acosx﹣1，由已知得：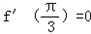
，
所以a=2，
所以f（x）=2sinx﹣x+b
①不等式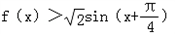
可化为：sinx﹣cosx﹣x＞﹣b
记函数g（x）=sinx﹣cosx﹣x，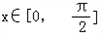
，
，
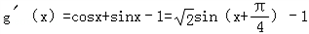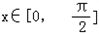所以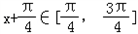
，
g'（x）＞0函数在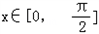
上是增函数，
最小值为g（0）=﹣1
所以b＞1，
所以b的取值范围是（1，+∞）
②由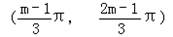
得：
，
所以m＞0
令f'（x）=2cosx﹣1＞0，可得
2kπ﹣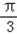
＜x＜2kπ+
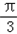，k∈Z
∵函数f（x）在区间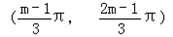
上是单调增函数，
∴
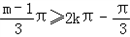且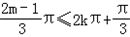
∴6k≤m≤3k+1
∵m＞0，
∴3k+1＞0，6k≤3k+1
∴k=0
∴0＜m≤1
求导函数可得：f'（x）=2cosx﹣1
令f'（x）＜0，可得cosx＜
∵x∈[0，π]，
∴
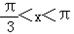
∴函数的单调减区间为
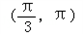
（2）f'（x）=acosx﹣1，由已知得：
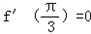，所以a=2，
所以f（x）=2sinx﹣x+b
①不等式
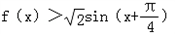可化为：sinx﹣cosx﹣x＞﹣b记函数g（x）=sinx﹣cosx﹣x，
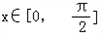
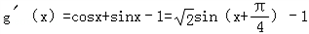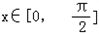，，所以
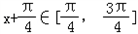，g'（x）＞0函数在
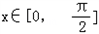上是增函数，最小值为g（0）=﹣1
所以b＞1，
所以b的取值范围是（1，+∞）
②由
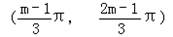得：，所以m＞0
令f'（x）=2cosx﹣1＞0，可得
2kπ﹣
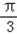＜x＜2kπ+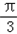，k∈Z∵函数f（x）在区间
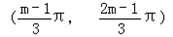上是单调增函数，∴
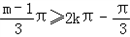且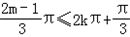∴6k≤m≤3k+1
∵m＞0，
∴3k+1＞0，6k≤3k+1
∴k=0
∴0＜m≤1
练习册系列答案
相关题目