题目内容
二次函数f(x)=ac2+bx+c(a、b、c∈Z)的图像按向量n=(-1,0)平移后关于y轴对称,方程f(x)-x=0的两根为α、β,且α∈(0,2),β∈(2,4),β-α=(1)求函数f(x)的解析式;
(2)设g(x)=x3-3x2-6x+m,若存在常数k,使得函数g(x)、f(x)在区间[-2,2]上的图像分别在直线y=k的上方和下方,试求实数m的取值范围.
解:(1)二次函数f(x)的对称轴为-![]()
∵左移1个单位后与y轴重合
∴-![]() =1,即b=-2a
=1,即b=-2a
f(x)=ax2-2ax+c 令H(x)=f(x)-x
即ax2-(2a+1)x+c=0的两根分别在(0,2)和(2,4)中
1 当a>0时,有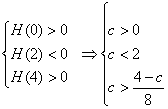
由∈Z得c=1,a>![]()
由|β-α|=![]()
解得a=1或a=-1(舍去) f(x)=x2-2x+1
2 当a<0时,有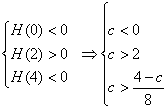 无解
无解
综上可知f(x)=x2-2x+1
(2)由题意,知当x∈[-2,2]上,f(x)max<g(x)min
当-2≤x≤2时,f(x)max=9 (9分)
![]() (x)=3x2-6x-6=3[x-(1-
(x)=3x2-6x-6=3[x-(1-![]() )][x-(1+
)][x-(1+![]() )]
)]
∵当x>1+![]() 时,
时,![]() (x)>0,在(1+
(x)>0,在(1+![]() ,+∞)上g(x)为增函数
,+∞)上g(x)为增函数
当1-![]() <x<1+
<x<1+![]() 时
时![]() (x)<0,在(1-
(x)<0,在(1-![]() ,1+
,1+![]() )上,g(x)为减函数
)上,g(x)为减函数
当x<1-![]() 时,
时,![]() (x)>0,在(-∞,1-
(x)>0,在(-∞,1-![]() )上g(x)为增函数
)上g(x)为增函数
∴g(x)在[-2,1-![]() ]上为增函数,在[1-
]上为增函数,在[1-![]() ,2]上是减函数
,2]上是减函数
又∵g(-2)=m-8,g(2)=m-16 ∴g(-2)>g(2)
∴在[-2,2]上,g(x)min=g(2)=m-16
∴m-16>9,即m>25

练习册系列答案
相关题目
设二次函数f(x)=x2+x+c(c>
)的图象与x轴的左右两个交点的横坐标分别为x1,x2,则x2-x1的取值范围为( )
| 1 |
| 8 |
| A、(0,1) | ||||||
B、(0,
| ||||||
C、(
| ||||||
D、(
|