Question

在对人们休闲方式的一次调查中，共调查120人，其中女性70人、男性50人，女性中有40人主要的休闲方式是看电视，另外30人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外30人主要的休闲方式是运动。

（1）根据以上数据建立一个2×2的列联表;

（2）在犯错误的概率不超过0.10的前提下，认为休闲方式与性别是否有关？

参考数据：独立性检验临界值表

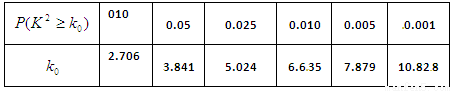
参考公式：独立性检验随机变量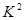值的计算公式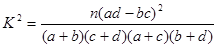：（其中）

 

Answer 1

【答案】

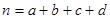（1）见解析（2）在犯错误的概率不超过0.10的前提下，认为休闲方式与性别有关

【解析】题考查做出列联表，考查利用观测值同临界值进行比较，得到休闲与性别无关的结论，本题是一个基础题，题目近几年的高考题中有机会出现，注意运算．

（1）根据所给的条件中的数据写出列联表，得到以运动为主要的休闲方式的比例为15：31．

（2）先假设休闲方式与性别无关，根据观测值的计算公式代入数据做出观测值，把所得的观测值同临界值进行比较，得到在犯错误的概率不超过0.1的前提下认为休闲方式与性别有关

解：（1）22的列连表为

        

休闲方式 性别	看电视	运动	总计
女性	40	30	70
男性	20	30	50
总计	60	60	120

　　　　　　　　　　　　　　　　　　　　　　　　………４分

（2）计算的观测值为

而2.706<3.428<3.841,

所以，在犯错误的概率不超过0.10的前提下，认为休闲方式与性别有关。１０分