题目内容
已知![]() 点
点![]()
(1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点,
①无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
②过![]() 作直线
作直线![]() 的垂线
的垂线![]()
求![]() 的取值范围
的取值范围
(1)由![]() 知,点
知,点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点的双曲线右支,由
为焦点的双曲线右支,由![]() 得
得![]() ,故轨迹
,故轨迹![]() 的方程为
的方程为![]() 3分
3分
(2)当直线![]() 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为![]()
与双曲线方程联立消去![]() 得:
得:![]()
∴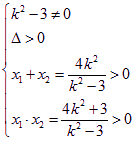 ,解得
,解得![]() ………………5分
………………5分
①![]()
![]()
∵![]() ,∴
,∴![]() ,
,
故得![]() 对任意的
对任意的![]() 恒成立,
恒成立,
∴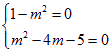 ,解得
,解得![]() ,∴当
,∴当![]() 时,
时,![]() ……………8分
……………8分
当直线![]() 的斜率不存在时,由
的斜率不存在时,由![]() 及
及![]() 知结论也成立
知结论也成立
综上,当![]() 时,
时,![]() ……………9分
……………9分
②∵![]() ,∴直线
,∴直线![]() 是双曲线右准线,
是双曲线右准线,
由双曲线定义得![]()
∴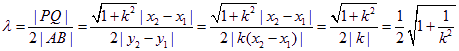
∵![]() ,∴
,∴![]() ,故
,故![]()
注意到直线的斜率不存在时,![]() ,此时
,此时![]()
综上,![]() ……………14分
……………14分
解析:
同答案

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目