题目内容
已知复数z1=i（1-i）3，复数z满足|z|=1，则|z-z1|的最大值是 ．
【答案】分析：化简复数z1为代数形式后，将z 设为三角形式，和复数z1的代数形式，共同代入|z-z1|，化简后可求最大值．
解答：解：z1=i（1-i）3=2-2i，
设z=cosα+isinα，
则z-z1=（cosα-2）+（sinα+2）i，|z-z1|2
=（cosα-2）2+（sinα+2）2=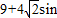
（ 
），
当sin（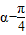
）=1时，|z-z1|2取得最大值 
．
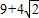从而得到|z-z1|的最大值为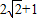
．
故答案为：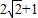
．
点评：本小题主要考查复数的代数表示法及其几何意义、复数基本性质和基本运算等基础知识，考查运算求解能力与转化思想．属于基础题．
解答：解：z1=i（1-i）3=2-2i，
设z=cosα+isinα，
则z-z1=（cosα-2）+（sinα+2）i，|z-z1|2
=（cosα-2）2+（sinα+2）2=
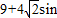（ ），当sin（
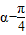）=1时，|z-z1|2取得最大值 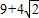．从而得到|z-z1|的最大值为
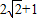．故答案为：
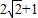．点评：本小题主要考查复数的代数表示法及其几何意义、复数基本性质和基本运算等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
小学课时作业全通练案系列答案
相关题目