题目内容
【题目】定义在![]() 上的函数
上的函数![]() 对任意
对任意![]() 都有
都有![]() ,且函数
,且函数![]() 的图象关于原点对称,若
的图象关于原点对称,若![]() 满足不等式
满足不等式![]() ,则当
,则当![]() 时,
时, ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵定义在R上的函数f(x)对任意x1,x2(x1≠x2)都有![]()
∴f(x)在R上单调递减,∵y=f(x+1)的图象关于原点对称,
∴y=f(x)的图象关于点(1,0)对称,∴f(1-x)=-f(1+x),
∴-f(2t-t2+2)=-f[1+(2t-t2+1)]=f[1-(2t-t2+1)]=f(t2-2t),
∵f(s2-2s)≤-f(2t-t2+2),∴f(s2-2s)≤f(t2-2t),
∵f(x)在R上单调递减,
∴s2-2s≥t2-2t∴(s-t)(s+t-2)≥0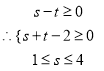 或
或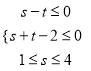
以s为横坐标,t为纵坐标建立平面直角坐标系,画出不等式组所表示的平面区域
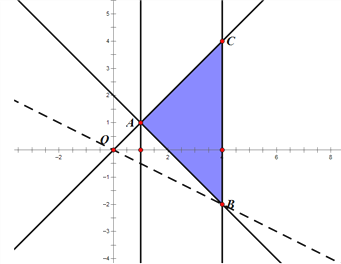
![]() 整理,得
整理,得![]() 直线
直线![]() 恒经过原点O(0,0)
恒经过原点O(0,0)
由图象可知kOB![]()
![]() 的取值范围是
的取值范围是![]()
故选D

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
