题目内容
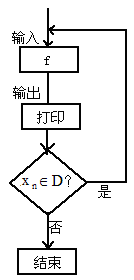
 (2001•上海)对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
(2001•上海)对任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:①输入数据x0∈D,经按列发生器,其工作原理如图:
②若x1∈D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去,现定义f(x)=
| 4x-2 |
| x+1 |
(Ⅰ)若输入x0=
| 49 |
| 65 |
(Ⅱ)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据x0的值;
(Ⅲ)若输入x0时,产生的无穷数列{xn}满足;对任意正整数n,均有xn>xn+1,求x0的取值范围.
分析:(1)确定f(x)的定义域,可得数列{xn}只有三项;
(2)由f(x)=
=x,可得结论;
(3)解不等式x<
,得x<-1或1<x<2,要使x1<x2,则x1<-1或1<x1<2,从而可求x0的取值范围.
(2)由f(x)=
| 4x-2 |
| x+1 |
(3)解不等式x<
| 4x-2 |
| x+1 |
解答:解:(1)∵f(x)的定义域D=(-∞,-1)∪(-1,+∞),
∴数列{xn}只有三项:x1=
,x2=
,x3=-1.…(3分)
(2)∵f(x)=
=x,即x2-3x+2=0,
∴x=1,或x=2.
即当x0=1或2时,xn+1=
=xn.
故当x0=1时,xn=1;当x0=2时,xn=2(n∈N).…(9分)
(3)解不等式x<
,得x<-1或1<x<2.
要使,x1<x2,则x1<-1或1<x1<2.…(12分)
对于函数f(x)=
=4-
,
若x1<-1,则x2=f(x1)>4,x3=f(x2)<x2.…(15分)
当1<x1<2时,x2=f(x),且1<x2<2,
依此类推,可得数列{xn}的所有项均满足xn+1>xn(n∈N).
综上所述,x1∈(1,2).
由x1=f(x0),得x0∈(1,2).…(18分)
∴数列{xn}只有三项:x1=
| 11 |
| 19 |
| 1 |
| 5 |
(2)∵f(x)=
| 4x-2 |
| x+1 |
∴x=1,或x=2.
即当x0=1或2时,xn+1=
| 4xn-2 |
| xn+1 |
故当x0=1时,xn=1;当x0=2时,xn=2(n∈N).…(9分)
(3)解不等式x<
| 4x-2 |
| x+1 |
要使,x1<x2,则x1<-1或1<x1<2.…(12分)
对于函数f(x)=
| 4x-2 |
| x+1 |
| 6 |
| x+1 |
若x1<-1,则x2=f(x1)>4,x3=f(x2)<x2.…(15分)
当1<x1<2时,x2=f(x),且1<x2<2,
依此类推,可得数列{xn}的所有项均满足xn+1>xn(n∈N).
综上所述,x1∈(1,2).
由x1=f(x0),得x0∈(1,2).…(18分)
点评:本题考查数列与函数的综合,考查新定义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
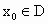 ,经数列发生器输出
,经数列发生器输出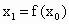 ;②若
;②若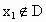 ,则数列发生器结束工作;若
,则数列发生器结束工作;若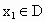 ,将
,将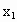 反馈回输入端,再输出
反馈回输入端,再输出 ,并依此规律进行下去.现定义
,并依此规律进行下去.现定义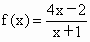 .
.
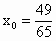 ,则由数列发生器产生数列
,则由数列发生器产生数列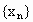 ,写出数列
,写出数列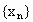 的所有项;
的所有项;
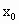 的值.
的值.