题目内容
17.在△ABC中,a,b,c分别为角A,B,C的对边,b=2,a=1,cosC=$\frac{3}{4}$.(1)求△ABC的周长;
(2)求sinA的值.
分析 (1)运用余弦定理,可得c,即可得到三角形的周长;
(2)运用同角的平方关系,可得sinC,再由正弦定理,即可得到sinA.
解答 解:(1)在△ABC中由余弦定理可知
c2=a2+b2-2abcosC=1+4-2×1×2×$\frac{3}{4}$=2,
∴$c=\sqrt{2}$,
∴△ABC的周长为a+b+c=$3+\sqrt{2}$;
(2)$sinC=\sqrt{1-{{cos}^2}C}=\frac{{\sqrt{7}}}{4}$,
在△ABC中由正弦定理可知 $\frac{a}{sinA}=\frac{c}{sinC}$,
∴$sinA=\frac{asinC}{c}=\frac{{\sqrt{14}}}{8}$.
点评 本题考查正弦定理和余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
8.已知等比数列{an}前n项和为Sn,则“a1>0”是“S2013>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.将四名青年志愿者安排到三个社区参加劳动,要求每个社区至少安排一名,则不同的安排方法种数是( )
| A. | 72 | B. | 36 | C. | 24 | D. | 12 |
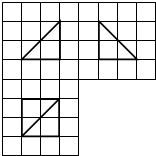 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的表面积为12π.
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体外接球的表面积为12π.