题目内容
已知函数f(x)=sinx-cosx,x∈R,则把导函数f′(x)的图象向左平移 个单位后得到的函数是
个单位后得到的函数是
- A.
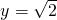 cosx
cosx - B.
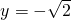 cosx
cosx - C.
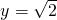 sinx
sinx - D.
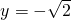 sinx
sinx
A
分析:求出原函数的导函数,化积后把解析式中的x换成x+ ,整理后可得要求的函数解析式.
,整理后可得要求的函数解析式.
解答:因为f(x)=sinx-cosx,则f′(x)=cosx+sinx= ,
,
把f′(x)的图象向左平移 个单位后得到的函数是y=
个单位后得到的函数是y= =
= .
.
故选A.
点评:本题考查了导数的加法与减法法则,同时考查了函数y=Asing(ωx+Φ)的图象平移问题,解答此题的关键是掌握“左加右减”的平移法则.
分析:求出原函数的导函数,化积后把解析式中的x换成x+
 ,整理后可得要求的函数解析式.
,整理后可得要求的函数解析式.解答:因为f(x)=sinx-cosx,则f′(x)=cosx+sinx=
 ,
,把f′(x)的图象向左平移
 个单位后得到的函数是y=
个单位后得到的函数是y= =
= .
.故选A.
点评:本题考查了导数的加法与减法法则,同时考查了函数y=Asing(ωx+Φ)的图象平移问题,解答此题的关键是掌握“左加右减”的平移法则.

练习册系列答案
相关题目
