题目内容
20.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{b}$=1(a>b>0)的左顶点A且斜率为k的直线交椭圆于另一个点B,且点B在x轴上的射影恰好为右焦点F,若0<k<$\frac{1}{3}$,则椭圆的离心率的取值范围是( )| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
分析 作出图形,则易知|AF2|=a+c,|BF2|=$\frac{{a}^{2}-{c}^{2}}{a}$,再由∠BAF2是直线的倾斜角,易得k=tan∠BAF2,然后通过0<k<$\frac{1}{3}$,分子分母同除a2得0<$\frac{1-{e}^{2}}{1+e}$<$\frac{1}{3}$求解.
解答 解:如图所示:|AF2|=a+c,|BF2|=$\frac{{a}^{2}-{c}^{2}}{a}$,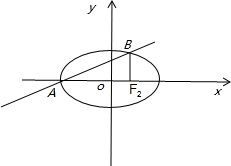
∴k=tan∠BAF2=$\frac{{a}^{2}-{c}^{2}}{a(a+c)}$,
又∵0<k<$\frac{1}{3}$,
∴0<$\frac{{a}^{2}-{c}^{2}}{a(a+c)}$<$\frac{1}{3}$,
∴0<$\frac{1-{e}^{2}}{1+e}$<$\frac{1}{3}$,
∴$\frac{2}{3}$<e<1.
故选:D.
点评 本题考查了椭圆与直线的位置关系及椭圆的几何性质和直线的斜率与倾斜角,难度不大,但需要灵活运用和转化知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.双曲线C的中心在原点,焦点在y轴上,离心率为$\sqrt{2}$,双曲线C与抛物线y2=4x的准线交于A,B两点,|AB|=4,则双曲线C的实轴长为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 4 | D. | $2\sqrt{3}$ |
5.已知全集U=R,M={x|x2<2x},则∁UM=( )
| A. | {x|X≥2} | B. | {x|x>2} | C. | {x|x≤0或x≥2} | D. | {x|0<x<2} |
12.在复平面上,复数z=a+bi(a,b∈R)与复数i(i-2)关于实轴对称,则a+b的值为( )
| A. | 1 | B. | -3 | C. | 3 | D. | 2 |